
Emil M.
Constantinescu
Computational Mathematician
emconsta[at]mcs.anl.gov
Office #: 2151
• LANS
• Mathematics and Computer Science
• Argonne National Laboratory
• Scientist at large at CASE
• University of Chicago
| Homepage | ||||||
|
||||||
| Publications |
Time-stepping methods are algorithms used to compute the numerical solution of ordinary differential equations as well as to evolve the solution of partial differential equations in time. This page describes three advanced techniques: general linear methods, implicit-explicit schemes, and multirate time-stepping algorithms. Implementations of varios algorithm is available in PETSc library.
Events, presentations, notes, ... of interes
- Extreme-scale solvers workshop 2012 (pdf)
- SIAM Presents (video)
- ITER (link)
- 1st International Workshop on High Order CFD Methods (link)
- Test problems (http://www.dm.uniba.it/~testset/testsetivpsolvers)
GLM | IMEX | Multirate - [Example] | Publications - [Journals - Proceedings - Reports] | Related links | Top
General linear (GL) methods, under various names (e.g., hybrid methods, pseudo Runge-Kutta) represent a natural generalization of both Runge-Kutta and linear multistep methods that are aimed at improving their stability and accuracy properties while taking advantage of past precomputed information. They use both internal stages like RK methods and information from previous solution steps like LM methods.
GLM | IMEX | Multirate - [Example] | Publications - [Journals - Proceedings - Reports] | Related links | Top
IMplicit-EXplicit (IMEX) time stepping methods
The dynamics of a process determines the best numerical solution strategy. Explicit
time discretizations are effective for slow processes as their computational cost per step is
relatively low. On the other hand implicit methods are more efficient for fast processes
as their step sizes are not limited by stability considerations. Time integration of
multiscale processes is challenging as neither purely explicit nor purely implicit methods are
adequate. Explicit methods require prohibitively small time steps (limited by the fastest
time scale in the system). Implicit methods require the solution of (non)linear systems of
equations that involve all the processes in the model; this is both computationally expensive
and difficult to implement. The implicit-explicit (IMEX) approach has been developed to alleviate these difficulties. The IMEX idea is to combine an implicit scheme for the stiff components with an explicit scheme for the non-stiff components such that the overall discretization method has the desired stability and accuracy properties.
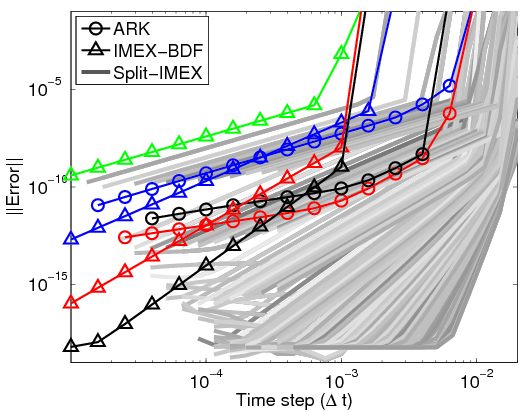
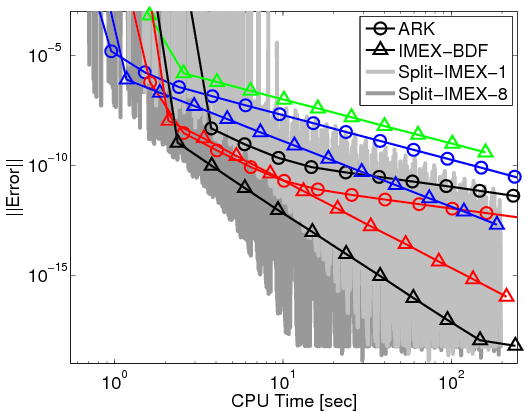
Below is a performance analysis of several extrapolation IMEX methods introduced in [Constantinescu and Sandu, 2008] applied to a advection-reaction problem with stiff boundary conditions. The comparison is carried among different IMEX-BDF and ARK methods of various orders. As discussed in the reference mentioned above, the extrapolation IMEX methods are easily parallelizable; therefore, a naive parallelization with OpenMP (left figure) shows that these methods can outperform the state-of-the-art BDF or Runge-Kutta IMEX schemes on a 8-core machine. [mode details are forthcoming]
 |
 |
GLM | IMEX | Multirate - [Example] | Publications - [Journals - Proceedings - Reports] | Related links | Top
Multirate time stepping methods
Hyperbolic conservation laws are of great practical importance as they model diverse physical phenomena that appear in mechanical and chemical engineering, aeronautics, astrophysics, meteorology and oceanography, financial modeling, environmental sciences, etc. Representative examples are gas dynamics, shallow water flow, groundwater flow, non-Newtonian flows, traffic flows, advection and dispersion of contaminants, etc. Conservative high resolution methods with explicit time discretization have gained widespread popularity to numerically solve these problems.Stability requirements limit the temporal step size, with the upper bound being determined by the ratio of the temporal and spatial meshes and the magnitude of the wave speed. Local spatial mesh refinement reduces the allowable time step for the explicit time discretizations. The time step for the entire domain is restricted by the finest mesh patch or by the highest wave velocity, and is typically (much) smaller than necessary for other variables in the computational domain.
Multirate time integration schemes allow the time step to vary across the spatial domain while satisfying the CFL condition only locally, resulting in substantially more efficient overall computations.
GLM | IMEX | Multirate - [Example] | Publications - [Journals - Proceedings - Reports] | Related links | Top
An example is given below that illustrates the main idea of multirate and AMR. The 2D simulation models the transport of a (power plant) plume in the atmosphere (1 km mixing layer) with an Eastern wind (5 m/s) and a turbulent diffusivity of 100 m2/s. The simulation is run for 6 hours. The power plant is turned off and the plume dynamics is simulated for another six hours. Note how the fine grid resolution follows the features of the solution. Such an algorithm that dynamically adapts the grid for large scale models is presented in [Constantinescu et al. 2007; Comp. Geosci.]. The fine resolution accurately resolves the fine features of the solution. In order to efficiently implement this AMR approach, different time steps should be used for different resolutions: large time steps for coarse resolutions and small time steps for fine resolutions resulting in multirate algorithms. Examples of such algorithms are found in [Constantinescu et al. 2007; Sci. Comp.] or [Sandu et al. 2007; Sci. Comp.]
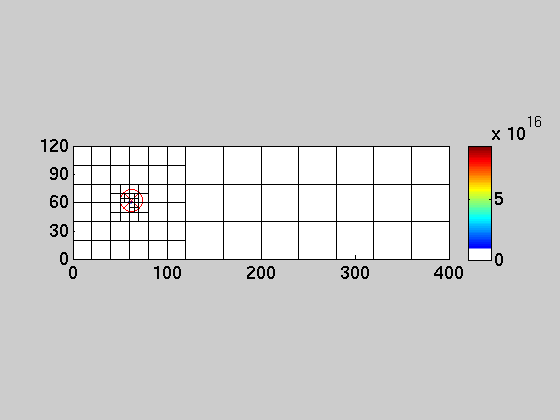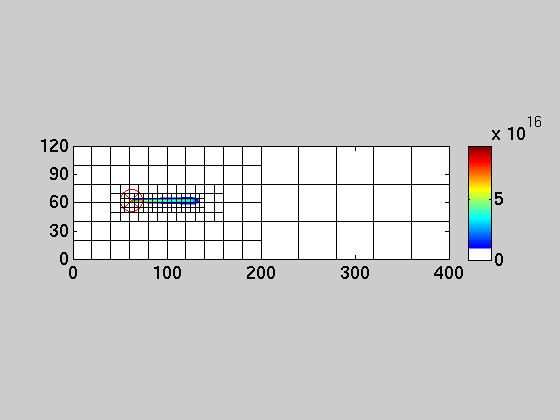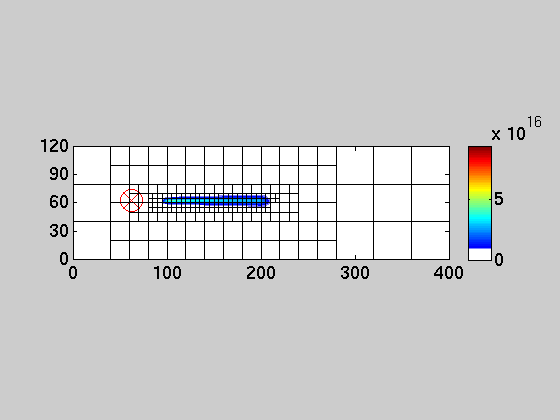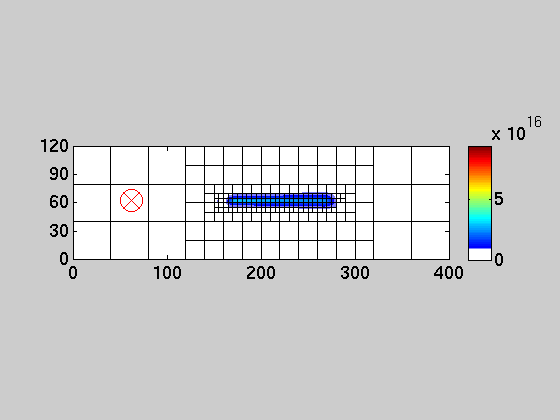
GLM | IMEX | Multirate - [Example] | Publications - [Journals - Proceedings - Reports] | Related links | Top
Selected journal publications, proceedings, presentations
Journal publications:

 Johann Rudi, Max Heldman, Emil M. Constantinescu, Qi Tang, and Xian-Zhu Tang,
"Scalable implicit solvers with dynamic mesh adaptation for a relativistic drift-kinetic Fokker-Planck-Boltzmann model."
Journal of Computational Physics, Vol. 507, Pages 112954, DOI: 10.1016/j.jcp.2024.112954, 2024.
[https://arxiv.org/abs/2303.17019]
Johann Rudi, Max Heldman, Emil M. Constantinescu, Qi Tang, and Xian-Zhu Tang,
"Scalable implicit solvers with dynamic mesh adaptation for a relativistic drift-kinetic Fokker-Planck-Boltzmann model."
Journal of Computational Physics, Vol. 507, Pages 112954, DOI: 10.1016/j.jcp.2024.112954, 2024.
[https://arxiv.org/abs/2303.17019]
 Shinhoo Kang and Emil M. Constantinescu,
"Enhancing Low-Order Discontinuous Galerkin Methods with Neural Ordinary Differential Equations for Compressible Navier--Stokes Equations."
Submitted, 2023.
[https://arxiv.org/abs/2310.18897v2]
Shinhoo Kang and Emil M. Constantinescu,
"Enhancing Low-Order Discontinuous Galerkin Methods with Neural Ordinary Differential Equations for Compressible Navier--Stokes Equations."
Submitted, 2023.
[https://arxiv.org/abs/2310.18897v2]

 Shinhoo Kang, Alp Dener, Aidan Hamilton, Hong Zhang, Emil M. Constantinescu, and Robert Jacob,
"Multirate Partitioned Runge-Kutta Methods for Coupled Navier-Stokes Equations."
Computers & Fluids, Volume 264 (15), DOI: https://doi.org/10.1016/j.compfluid.2023.105964, 2023.
[https://arxiv.org/abs/2202.11890]
Shinhoo Kang, Alp Dener, Aidan Hamilton, Hong Zhang, Emil M. Constantinescu, and Robert Jacob,
"Multirate Partitioned Runge-Kutta Methods for Coupled Navier-Stokes Equations."
Computers & Fluids, Volume 264 (15), DOI: https://doi.org/10.1016/j.compfluid.2023.105964, 2023.
[https://arxiv.org/abs/2202.11890]
-

 Shinhoo Kang and Emil M. Constantinescu,
"Learning subgrid-scale models with neural ordinary differential equations."
Computers and Fluids, In Press, Vol. 261, Pages 105919, DOI: 10.1016/j.compfluid.2023.105919.
[https://arxiv.org/abs/2212.09967]
Shinhoo Kang and Emil M. Constantinescu,
"Learning subgrid-scale models with neural ordinary differential equations."
Computers and Fluids, In Press, Vol. 261, Pages 105919, DOI: 10.1016/j.compfluid.2023.105919.
[https://arxiv.org/abs/2212.09967]
 Daniel Adrian Maldonado, Emil M. Constantinescu, Junbo Zhao, and Mihai Anitescu,
"Computationally efficient power system maximum transient linear growth estimation."
Submitted, 2023.
[https://arxiv.org/abs/2302.10388]
Daniel Adrian Maldonado, Emil M. Constantinescu, Junbo Zhao, and Mihai Anitescu,
"Computationally efficient power system maximum transient linear growth estimation."
Submitted, 2023.
[https://arxiv.org/abs/2302.10388]
-

 Youngdae Kim, Debojyoti Ghosh, Emil Constantinescu, and Ramesh Balakrishnan,
"GPU-Accelerated WENO schemes for the DNS of compressible turbulent flows."
Computers & Fluids, Vol 251, Pages 105744, 2023.
(DOI: 10.1016/j.compfluid.2022.105744).
[https://arxiv.org/abs/2211.16718]
Youngdae Kim, Debojyoti Ghosh, Emil Constantinescu, and Ramesh Balakrishnan,
"GPU-Accelerated WENO schemes for the DNS of compressible turbulent flows."
Computers & Fluids, Vol 251, Pages 105744, 2023.
(DOI: 10.1016/j.compfluid.2022.105744).
[https://arxiv.org/abs/2211.16718]
-

 Hong Zhang and Emil M. Constantinescu,
"Optimal checkpointing for adjoint multistage time-stepping schemes."
Journal of Computational Science, Vol 366, 101913, (DOI: 10.1016/j.jocs.2022.101913).
[https://arxiv.org/abs/2106.13879]
Hong Zhang and Emil M. Constantinescu,
"Optimal checkpointing for adjoint multistage time-stepping schemes."
Journal of Computational Science, Vol 366, 101913, (DOI: 10.1016/j.jocs.2022.101913).
[https://arxiv.org/abs/2106.13879]
-

 Emil Constantinescu,
"Implicit extensions of an explicit multirate Runge–Kutta scheme."
Applied Mathematics Letters, Vol 128, Pages 107871, 2022.
(DOI: 10.1016/j.aml.2021.107871).
[https://arxiv.org/abs/2112.10568]
Emil Constantinescu,
"Implicit extensions of an explicit multirate Runge–Kutta scheme."
Applied Mathematics Letters, Vol 128, Pages 107871, 2022.
(DOI: 10.1016/j.aml.2021.107871).
[https://arxiv.org/abs/2112.10568]

 Adrian Maldonado, Emil M. Constantinescu, Hong Zhang, Vishwas Rao, and Mihai Anitescu,
"Trust-region approximation of extreme trajectories in power system dynamics." IEEE Transactions on Power Systems , Vol 37(5), Pages 3937-3946, 2022.
[https://arxiv.org/abs/2106.16132]
Adrian Maldonado, Emil M. Constantinescu, Hong Zhang, Vishwas Rao, and Mihai Anitescu,
"Trust-region approximation of extreme trajectories in power system dynamics." IEEE Transactions on Power Systems , Vol 37(5), Pages 3937-3946, 2022.
[https://arxiv.org/abs/2106.16132]

 Shinhoo Kang and Emil M. Constantinescu,
"Entropy-preserving and entropy-stable relaxation IMEX and multirate time-stepping methods."
Journal of Scientific Computing, Vol. 93(23), DOI: 10.1007/s10915-022-01982-w, 2022.
[https://arxiv.org/abs/2108.08908]
Shinhoo Kang and Emil M. Constantinescu,
"Entropy-preserving and entropy-stable relaxation IMEX and multirate time-stepping methods."
Journal of Scientific Computing, Vol. 93(23), DOI: 10.1007/s10915-022-01982-w, 2022.
[https://arxiv.org/abs/2108.08908]
-
Hong Zhang, Zhengyu Liu, Emil M. Constantinescu, and Robert Jacob
"Stability Analysis of Coupled Advection-Diffusion Models with Bulk Interface Condition"
Journal of Scientific Computing , Vol 93(33), DOI: 10.1007/s10915-022-01983-9, 2022.

 Alina Kononov, Cheng-Wei Lee, Tatiane Pereira dos Santos, Brian Robinson, Yifan Yao, Yi Yao, Xavier Andrade, Andrew David Baczewski, Emil Constantinescu, Alfredo Correa, Yosuke Kanai, Norman Modine, and Andre Schleife,
"Electron dynamics in extended systems within real-time time-dependent density functional theory, "
MRS Communications, Pages 1-13, DOI: 10.1557/s43579-022-00273-7, 2022.
[https://arxiv.org/abs/2205.04386]
Alina Kononov, Cheng-Wei Lee, Tatiane Pereira dos Santos, Brian Robinson, Yifan Yao, Yi Yao, Xavier Andrade, Andrew David Baczewski, Emil Constantinescu, Alfredo Correa, Yosuke Kanai, Norman Modine, and Andre Schleife,
"Electron dynamics in extended systems within real-time time-dependent density functional theory, "
MRS Communications, Pages 1-13, DOI: 10.1557/s43579-022-00273-7, 2022.
[https://arxiv.org/abs/2205.04386]
-
 Luisa D'amore, Emil Constantinescu, and Luisa Carracciuolo,
"A scalable space-time domain decomposition approach for solving large scale non linear regularized inverse ill posed problems in 4D Variational Data Assimilation, " 91(59),
Springer Journal of Scientific Computing, 2022.
Luisa D'amore, Emil Constantinescu, and Luisa Carracciuolo,
"A scalable space-time domain decomposition approach for solving large scale non linear regularized inverse ill posed problems in 4D Variational Data Assimilation, " 91(59),
Springer Journal of Scientific Computing, 2022.

 Shinhoo Kang, Emil M. Constantinescu, Hong Zhang, and Robert Jacob,
"Mass-Conserving Implicit-Explicit Methods for Coupled Compressible Navier-Stokes Equations."
Computer Methods in Applied Mechanics and Engineering (CMAME), Vol 384, pp. 113988, 2021, (DOI: 10.1016/j.cma.2021.113988).
[https://arxiv.org/abs/2101.09263]
Shinhoo Kang, Emil M. Constantinescu, Hong Zhang, and Robert Jacob,
"Mass-Conserving Implicit-Explicit Methods for Coupled Compressible Navier-Stokes Equations."
Computer Methods in Applied Mechanics and Engineering (CMAME), Vol 384, pp. 113988, 2021, (DOI: 10.1016/j.cma.2021.113988).
[https://arxiv.org/abs/2101.09263]
-

 Hong Zhang, Emil M. Constantinescu, and Barry F. Smith, "PETSc TSAdjoint: a discrete adjoint ODE solver for first-order and second-order sensitivity analysis."
SIAM Journal of Scientific Computing, Vol 44, Pages C1-C24, 2022.
[https://arxiv.org/abs/1912.07696]
Hong Zhang, Emil M. Constantinescu, and Barry F. Smith, "PETSc TSAdjoint: a discrete adjoint ODE solver for first-order and second-order sensitivity analysis."
SIAM Journal of Scientific Computing, Vol 44, Pages C1-C24, 2022.
[https://arxiv.org/abs/1912.07696]
-

 Hong Zhang, Zhengyu Liu, Emil M. Constantinescu, and Robert Jacob,
"Stability analysis of interface conditions for ocean-atmosphere coupling."
Springer Journal of Scientific Computing, Vol. 84 (44), 2020.
[https://arxiv.org/abs/1909.00916]
Hong Zhang, Zhengyu Liu, Emil M. Constantinescu, and Robert Jacob,
"Stability analysis of interface conditions for ocean-atmosphere coupling."
Springer Journal of Scientific Computing, Vol. 84 (44), 2020.
[https://arxiv.org/abs/1909.00916] - Valeria Mele, Emil M. Constantinescu, Luisa Carracciuolo, and Luisa D'Amore, "A PETSc parallel-in-time solver based on MGRIT algorithm." Submitted, Concurrency and Computation: Practice and Experience, 2018.
 Shrirang Abhyankar, Jed Brown, Emil M. Constantinescu, Debojyoti Ghosh*, Barry F. Smith and Hong Zhang*, "PETSc/TS: A modern scalable ODE/DAE solver library." Submitted, 2018. [https://arxiv.org/abs/1806.01437]
Shrirang Abhyankar, Jed Brown, Emil M. Constantinescu, Debojyoti Ghosh*, Barry F. Smith and Hong Zhang*, "PETSc/TS: A modern scalable ODE/DAE solver library." Submitted, 2018. [https://arxiv.org/abs/1806.01437]
-

 Simone Marras, Michal A. Kopera, Emil M. Constantinescu, Jenny
Suckale, and Francis X. Giraldo "A residual-based shock capturing scheme for the continuous/discontinuous spectral element solution of the 2D shallow water equations." Vol. 114, Pages 45-63, 2018. [http://arxiv.org/abs/1607.04547]
Simone Marras, Michal A. Kopera, Emil M. Constantinescu, Jenny
Suckale, and Francis X. Giraldo "A residual-based shock capturing scheme for the continuous/discontinuous spectral element solution of the 2D shallow water equations." Vol. 114, Pages 45-63, 2018. [http://arxiv.org/abs/1607.04547] -

 Emil Constantinescu, "Generalizing global error estimation for ordinary differential equations by using coupled time-stepping methods." Journal of Computational and Applied Mathematics, Vol 332(C), Pages 140-158, 2018. (https://arxiv.org/abs/1503.05166)
Emil Constantinescu, "Generalizing global error estimation for ordinary differential equations by using coupled time-stepping methods." Journal of Computational and Applied Mathematics, Vol 332(C), Pages 140-158, 2018. (https://arxiv.org/abs/1503.05166) -

 Shrirang Abhyankar, Emil M. Constantinescu, Barry Smith, Alexander J. Flueck, and Daniel A. Maldonado "Parallel dynamics simulation using a Krylov-Schwarz linear solution scheme." IEEE Transactions on Smart Grid Special Issue on High Performance Computing (HPC) Applications for a More Resilient and Efficient Power Grid, Vol. 8(3), Pages 1378-1386, 2017.
Shrirang Abhyankar, Emil M. Constantinescu, Barry Smith, Alexander J. Flueck, and Daniel A. Maldonado "Parallel dynamics simulation using a Krylov-Schwarz linear solution scheme." IEEE Transactions on Smart Grid Special Issue on High Performance Computing (HPC) Applications for a More Resilient and Efficient Power Grid, Vol. 8(3), Pages 1378-1386, 2017.
-

 Hong Zhang*, Shrirang S. Abhyankar, Emil M. Constantinescu, and Mihai Anitescu, "Discrete adjoint sensitivity analysis of power system dynamics." IEEE Transactions on Circuits and Systems--I: Regular Papers, Vol. 64(5), Pages 1247-1259, 2017.
Hong Zhang*, Shrirang S. Abhyankar, Emil M. Constantinescu, and Mihai Anitescu, "Discrete adjoint sensitivity analysis of power system dynamics." IEEE Transactions on Circuits and Systems--I: Regular Papers, Vol. 64(5), Pages 1247-1259, 2017. -

 Noemi Petra, Cosmin G. Petra, Zheng Zhang*, Emil M. Constantinescu, and Mihai Anitescu, "A Bayesian approach for parameter estimation with uncertainty for dynamic power systems." IEEE Transactions on Power Systems, Vol. 32(4), Pages 2735-2743, 2017.
Noemi Petra, Cosmin G. Petra, Zheng Zhang*, Emil M. Constantinescu, and Mihai Anitescu, "A Bayesian approach for parameter estimation with uncertainty for dynamic power systems." IEEE Transactions on Power Systems, Vol. 32(4), Pages 2735-2743, 2017. -


 Debojyoti Ghosh* and Emil M. Constantinescu, "Semi-implicit time integration of atmospheric flows with characteristic-based flux partitioning." SIAM Journal on Scientific Computing (SISC), Vol. 38(3), Pages A1848-A1875, 2016. [Preprint # ANL/MCS-P5417-1015; http://arxiv.org/abs/1510.05751].
Debojyoti Ghosh* and Emil M. Constantinescu, "Semi-implicit time integration of atmospheric flows with characteristic-based flux partitioning." SIAM Journal on Scientific Computing (SISC), Vol. 38(3), Pages A1848-A1875, 2016. [Preprint # ANL/MCS-P5417-1015; http://arxiv.org/abs/1510.05751]. -

 Debojyoti Ghosh* and Emil M. Constantinescu, "A well-balanced conservative finite-difference algorithm for atmospheric flows." AAIA Journal, Accepted, 2015. [Preprint # ANL/MCS-P5371-0615].
Debojyoti Ghosh* and Emil M. Constantinescu, "A well-balanced conservative finite-difference algorithm for atmospheric flows." AAIA Journal, Accepted, 2015. [Preprint # ANL/MCS-P5371-0615]. -


 Debojyoti Ghosh*, Emil M. Constantinescu, and Jed Brown, "Efficient implementation of non-linear compact schemes on massively-parallel platforms." SIAM Journal on Scientific Computing (SISC), Vol. 37(3), Pages C354-C383, 2015. ->
Debojyoti Ghosh*, Emil M. Constantinescu, and Jed Brown, "Efficient implementation of non-linear compact schemes on massively-parallel platforms." SIAM Journal on Scientific Computing (SISC), Vol. 37(3), Pages C354-C383, 2015. -> 
 Technical report version.
Technical report version. -

 Francis X Giraldo, James F. Kelly, and Emil Constantinescu, "Implicit-explicit formulations of a three-dimensional nonhydrostatic unified model of the atmosphere (NUMA)." SIAM Journal on Scientific Computing (SISC), In press, Preprint # ANL/MCS-P2083-0512, 2013.
Francis X Giraldo, James F. Kelly, and Emil Constantinescu, "Implicit-explicit formulations of a three-dimensional nonhydrostatic unified model of the atmosphere (NUMA)." SIAM Journal on Scientific Computing (SISC), In press, Preprint # ANL/MCS-P2083-0512, 2013. -


 Emil M. Constantinescu and Adrian Sandu, "Extrapolated multirate methods for differential equations with multiple time scales." Journal of
Scientific Computing, Vol. 56(1), pp 28-44, 2013.
Emil M. Constantinescu and Adrian Sandu, "Extrapolated multirate methods for differential equations with multiple time scales." Journal of
Scientific Computing, Vol. 56(1), pp 28-44, 2013.
-

 David E. Keyes, Lois Curfman McInnes, Carol Woodward, William Gropp, Eric Myra, Michael Pernice,
John Bell, Jed Brown, Alain Clo, Jeffrey Connors, Emil Constantinescu, Don Estep, Kate Evans,
Charbel Farhat, Ammar Hakim, Glenn Hammond, Glen Hansen, Judith Hill, Tobin Isaac, Xiaomin Jiao, Kirk Jordan,
Dinesh Kaushik, Efthimios Kaxiras, Alice Koniges, Kihwan Lee, Aaron Lott, Qiming Lu, John Magerlein,
Reed Maxwell, Michael McCourt, Miriam Mehl, Roger Pawlowski, Amanda Peters Randles, Daniel Reynolds,
Beatrice Rivière, Ulrich Rüde, Tim Scheibe, John Shadid, Brendan Sheehan, Mark Shephard, Andrew Siegel,
Barry Smith, Xianzhu Tang, Cian Wilson, and Barbara Wohlmuth "Multiphysics Simulations: Challenges and Opportunities." International Journal of High Performance Computing Applications, 27(1): 4-83, 2013.
-->> Tech Report verion:
David E. Keyes, Lois Curfman McInnes, Carol Woodward, William Gropp, Eric Myra, Michael Pernice,
John Bell, Jed Brown, Alain Clo, Jeffrey Connors, Emil Constantinescu, Don Estep, Kate Evans,
Charbel Farhat, Ammar Hakim, Glenn Hammond, Glen Hansen, Judith Hill, Tobin Isaac, Xiaomin Jiao, Kirk Jordan,
Dinesh Kaushik, Efthimios Kaxiras, Alice Koniges, Kihwan Lee, Aaron Lott, Qiming Lu, John Magerlein,
Reed Maxwell, Michael McCourt, Miriam Mehl, Roger Pawlowski, Amanda Peters Randles, Daniel Reynolds,
Beatrice Rivière, Ulrich Rüde, Tim Scheibe, John Shadid, Brendan Sheehan, Mark Shephard, Andrew Siegel,
Barry Smith, Xianzhu Tang, Cian Wilson, and Barbara Wohlmuth "Multiphysics Simulations: Challenges and Opportunities." International Journal of High Performance Computing Applications, 27(1): 4-83, 2013.
-->> Tech Report verion: 
-

 D.E. Keyes, L.C. McInnes, C. Woodward, W.D. Gropp, E. Myra, M. Pernice, J. Bell, J. Brown, A. Clo, J. Connors, E. Constantinescu, D. Estep, K. Evans, C. Farhat, A. Hakim, G. Hammond, G. Hansen, J. Hill, T. Isaac, X. Jiao, K. Jordan, D. Kaushik, E. Kaxiras, A. Koniges, K. Lee, A. Lott, Q. Lu, J. Magerlein, R. Maxwell, M. McCourt, M. Mehl, R. Pawlowski, A. Peters, D. Reynolds, B. Rivière, U. Rüde, T. Scheibe, J. Shadid, B. Sheehan, M. Shephard, A. Siegel, B. Smith, X. Tang, C. Wilson, B. Wohlmuth, "Multiphysics Simulations: Challenges and Opportunities." Tech. Rep. ANL/MCS-TM-321, Revision 1.1, October 2012, Argonne National Laboratory. ICiS Multiphysics 2011 Workshop Report, Park City, Utah, July 30 - August 6, 2012. To appear as a special issue of the International Journal of High Performance Computing Applications.
D.E. Keyes, L.C. McInnes, C. Woodward, W.D. Gropp, E. Myra, M. Pernice, J. Bell, J. Brown, A. Clo, J. Connors, E. Constantinescu, D. Estep, K. Evans, C. Farhat, A. Hakim, G. Hammond, G. Hansen, J. Hill, T. Isaac, X. Jiao, K. Jordan, D. Kaushik, E. Kaxiras, A. Koniges, K. Lee, A. Lott, Q. Lu, J. Magerlein, R. Maxwell, M. McCourt, M. Mehl, R. Pawlowski, A. Peters, D. Reynolds, B. Rivière, U. Rüde, T. Scheibe, J. Shadid, B. Sheehan, M. Shephard, A. Siegel, B. Smith, X. Tang, C. Wilson, B. Wohlmuth, "Multiphysics Simulations: Challenges and Opportunities." Tech. Rep. ANL/MCS-TM-321, Revision 1.1, October 2012, Argonne National Laboratory. ICiS Multiphysics 2011 Workshop Report, Park City, Utah, July 30 - August 6, 2012. To appear as a special issue of the International Journal of High Performance Computing Applications. -


 Emil M. Constantinescu and Adrian Sandu, "Optimal strong-stability-preserving general linear methods." SIAM Journal of
Scientific Computing, Vol. 32(5), Pages 3130-3150, 2010. ->
Emil M. Constantinescu and Adrian Sandu, "Optimal strong-stability-preserving general linear methods." SIAM Journal of
Scientific Computing, Vol. 32(5), Pages 3130-3150, 2010. -> 
 Technical report with complete results.
Technical report with complete results. -


 Emil M. Constantinescu and Adrian Sandu, "Extrapolated implicit-explicit time stepping." Vol. 31(6), Pages 4452-4477, SIAM Journal of
Scientific Computing, 2010. ->
Emil M. Constantinescu and Adrian Sandu, "Extrapolated implicit-explicit time stepping." Vol. 31(6), Pages 4452-4477, SIAM Journal of
Scientific Computing, 2010. -> 
 Technical report version.
Technical report version. -

 Emil M. Constantinescu, "On the order of general linear methods." Vol. 22(9), Pages 1425-1428, Applied Mathematics Letters, 2009. ->
Emil M. Constantinescu, "On the order of general linear methods." Vol. 22(9), Pages 1425-1428, Applied Mathematics Letters, 2009. -> 
 Technical report version [ANL/MCS-P1555-1008, Oct 2008].
Technical report version [ANL/MCS-P1555-1008, Oct 2008]. -

 Adrian Sandu and Emil M. Constantinescu, "Multirate explicit Adams methods for time integration of conservation laws." Vol. 38(2), Pages 229-249, Journal of
Scientific Computing, 2009. ->
Adrian Sandu and Emil M. Constantinescu, "Multirate explicit Adams methods for time integration of conservation laws." Vol. 38(2), Pages 229-249, Journal of
Scientific Computing, 2009. ->

 Technical report version.
Technical report version. -


 Emil M. Constantinescu, Adrian Sandu, and Gregory R. Carmichael, "Modeling atmospheric chemistry and transport with dynamic adaptive resolution." Vol. 12(2), Pages 133-151,
Computational Geosciences, 2008.
Emil M. Constantinescu, Adrian Sandu, and Gregory R. Carmichael, "Modeling atmospheric chemistry and transport with dynamic adaptive resolution." Vol. 12(2), Pages 133-151,
Computational Geosciences, 2008. -

 Emil M. Constantinescu and Adrian Sandu, "Multirate timestepping
methods for hyperbolic conservation laws." Vol. 33(3), Pages 239-278, Journal of
Scientific Computing, 2007. ->
Emil M. Constantinescu and Adrian Sandu, "Multirate timestepping
methods for hyperbolic conservation laws." Vol. 33(3), Pages 239-278, Journal of
Scientific Computing, 2007. -> 
 Technical report version.
Technical report version.
GLM | IMEX | Multirate - [Example] | Publications - [Journals - Proceedings - Reports] | Related links | Top
Proceedings/Presentations/Posters:
-


 Debojyoti Ghosh* and Emil M. Constantinescu, "Nonlinear compact finite-difference schemes with semi-implicit time stepping."Springer's Lecture Notes in Computational Science and Engineering (LNCSE) Series, ICOSAHOM 2014, Vol. 106, Pages 237-245, 2015.
Debojyoti Ghosh* and Emil M. Constantinescu, "Nonlinear compact finite-difference schemes with semi-implicit time stepping."Springer's Lecture Notes in Computational Science and Engineering (LNCSE) Series, ICOSAHOM 2014, Vol. 106, Pages 237-245, 2015. 

 Shrirang Abhyankar*, Barry Smith, and Emil M. Constantinescu, "Evaluation of overlapping restricted additive Schwarz preconditioning for parallel solution of very large power flow problems." Proceedings of the 3rd International Workshop on High Performance Computing, Networking and Analytics for the Power Grid, pp 5:1-5:8, 2013.
Shrirang Abhyankar*, Barry Smith, and Emil M. Constantinescu, "Evaluation of overlapping restricted additive Schwarz preconditioning for parallel solution of very large power flow problems." Proceedings of the 3rd International Workshop on High Performance Computing, Networking and Analytics for the Power Grid, pp 5:1-5:8, 2013.
-
Emil M. Constantinescu, "High Order Partitioned Time Stepping Methods for Stiff Problems" at SIAM Computational Science and Engineering (CS&E) (SIAM CSE13), Boston, MA, Feb 25 - Mar 1, 2013.
-
Emil M. Constantinescu, "Consistency and stability considerations for implicit-explicit additive splittings" at SIAM Annual Meeting (SIAM AN12), Minneapolis, MN, July 9-13, 2012.
-

 Barry Smith, Lois Curfman McInnes, Emil Constantinescu, Mark Adams, Satish Balay, Jed Brown, Matthew Knepley, and Hong Zhang, "PETSc's Software Strategy for the Design Space of Composable Extreme-Scale Solvers." (Preprint # ANL/MCS-P2059-0312) DOE Exascale Research Conference, April 16-18, 2012, Portland, OR, 2012.
Barry Smith, Lois Curfman McInnes, Emil Constantinescu, Mark Adams, Satish Balay, Jed Brown, Matthew Knepley, and Hong Zhang, "PETSc's Software Strategy for the Design Space of Composable Extreme-Scale Solvers." (Preprint # ANL/MCS-P2059-0312) DOE Exascale Research Conference, April 16-18, 2012, Portland, OR, 2012. -
Emil M. Constantinescu and Adrian Sandu, "Multirate explicit SSP methods for hyperbolic PDEs" in Time Discretizations for the Evolution of Time-dependent PDEs mini-symposium; SIAM Annual Meeting (AN10), Pittsburgh, PA, July 13, 2010.
-

 Adrian Sandu and Emil M. Constantinescu, "Multirate time discretizations for hyperbolic partial differential equations." International Conference of Numerical Analysis and Applied Mathematics (ICNAAM 2009), Crete, Greece, 18-22 September; Vol. 1168(1), pp. 1411-1414, 2009.
Adrian Sandu and Emil M. Constantinescu, "Multirate time discretizations for hyperbolic partial differential equations." International Conference of Numerical Analysis and Applied Mathematics (ICNAAM 2009), Crete, Greece, 18-22 September; Vol. 1168(1), pp. 1411-1414, 2009. -
 Emil M. Constantinescu
and Adrian Sandu, "Explicit time stepping methods with high stage order and monotonicity properties."
International Conference on Computational Science (ICCS) 2009, Baton Rouge, Louisiana,
May 25-27, 2009 [
Emil M. Constantinescu
and Adrian Sandu, "Explicit time stepping methods with high stage order and monotonicity properties."
International Conference on Computational Science (ICCS) 2009, Baton Rouge, Louisiana,
May 25-27, 2009 [  Preprint ANL/MCS-P1576-0109, January 2009].
Preprint ANL/MCS-P1576-0109, January 2009]. -
"On General Linear Time Stepping Methods." Presented by Emil M. Constantinescu at SIAM CS&E 2009 meeting, Miami, FL, March 2-6, 2009.
-

 Emil M. Constantinescu and Adrian Sandu, "On Extrapolated multirate numerical integration methods."
ECMI 2008 (Springer Mathematics in Industry), 2008 ->
Emil M. Constantinescu and Adrian Sandu, "On Extrapolated multirate numerical integration methods."
ECMI 2008 (Springer Mathematics in Industry), 2008 -> 
 Technical report version.
Technical report version. -
 Emil M. Constantinescu and Adrian Sandu,
"Strong stability preserving multirate schemes for hyperbolic conservation
laws." SIAM Conference on Computational Science and Engineering (CSE
2007), Costa Mesa, CA, February
18-23, 2007.
Emil M. Constantinescu and Adrian Sandu,
"Strong stability preserving multirate schemes for hyperbolic conservation
laws." SIAM Conference on Computational Science and Engineering (CSE
2007), Costa Mesa, CA, February
18-23, 2007. -
 Emil M. Constantinescu
and Adrian Sandu, "On adaptive mesh refinement for atmospheric pollution
models." International Conference on Computational Science (ICCS) 2005, pages 798-806 Atlanta, GA,
May 22-25, 2005.
Emil M. Constantinescu
and Adrian Sandu, "On adaptive mesh refinement for atmospheric pollution
models." International Conference on Computational Science (ICCS) 2005, pages 798-806 Atlanta, GA,
May 22-25, 2005.  Emil M. Constantinescu, Wenyuan Liao,
and Adrian Sandu, "Mesh refinement strategies in air quality modeling." High Performance Computing Symposium
(HPC) 2005, pages 158-163 - San Diego, CA, April 2-8, 2005.
Emil M. Constantinescu, Wenyuan Liao,
and Adrian Sandu, "Mesh refinement strategies in air quality modeling." High Performance Computing Symposium
(HPC) 2005, pages 158-163 - San Diego, CA, April 2-8, 2005.
GLM | IMEX | Multirate - [Example] | Publications - [Journals - Proceedings - Reports] | Related links | Top
-

 Emil M. Constantinescu and Adrian Sandu, "Optimal Explicit Strong-Stability-Preserving General Linear Methods: Complete Results." Mathematics and Computer Science Division Technical Memorandum ANL/MCS-TM-304, Argonne National Laboratory, January 2009.
Emil M. Constantinescu and Adrian Sandu, "Optimal Explicit Strong-Stability-Preserving General Linear Methods: Complete Results." Mathematics and Computer Science Division Technical Memorandum ANL/MCS-TM-304, Argonne National Laboratory, January 2009. -

 Emil M. Constantinescu and Adrian Sandu, "On the order of general linear methods." Technical Report ANL/MCS/JA-62914, Mathematics and Computer Science, Argonne National Laboratory, Oct 2008.
Emil M. Constantinescu and Adrian Sandu, "On the order of general linear methods." Technical Report ANL/MCS/JA-62914, Mathematics and Computer Science, Argonne National Laboratory, Oct 2008. 
 Emil M. Constantinescu and Adrian Sandu, "On Extrapolated Multirate Methods." Technical Report TR-08-12, Computer
Science, Virginia Tech, 2008.
Emil M. Constantinescu and Adrian Sandu, "On Extrapolated Multirate Methods." Technical Report TR-08-12, Computer
Science, Virginia Tech, 2008.
 Emil M. Constantinescu and Adrian Sandu, "Achieving Very High Order for Implicit Explicit Time Stepping: Extrapolation Methods."Mathematics and Computer Science Division Technical Memorandum ANL/MCS-TM-306, Argonne National Laboratory, April 2009.
Emil M. Constantinescu and Adrian Sandu, "Achieving Very High Order for Implicit Explicit Time Stepping: Extrapolation Methods."Mathematics and Computer Science Division Technical Memorandum ANL/MCS-TM-306, Argonne National Laboratory, April 2009.-

 Adrian Sandu and Emil M. Constantinescu, "Multirate explicit Adams methods for time integration of conservation laws." Technical Report TR-07-30(989), Computer
Science, Virginia Tech, 2007.
Adrian Sandu and Emil M. Constantinescu, "Multirate explicit Adams methods for time integration of conservation laws." Technical Report TR-07-30(989), Computer
Science, Virginia Tech, 2007. -

 Emil M.
Constantinescu and Adrian Sandu, "Update on multirate timestepping
methods for hyperbolic conservation laws." Technical Report TR-07-12(955), Computer
Science, Virginia Tech, 2007.
Emil M.
Constantinescu and Adrian Sandu, "Update on multirate timestepping
methods for hyperbolic conservation laws." Technical Report TR-07-12(955), Computer
Science, Virginia Tech, 2007. -

 Emil M.
Constantinescu and Adrian Sandu, "Multirate timestepping
methods for hyperbolic conservation laws." Technical Report TR-06-15, Computer
Science, Virginia Tech, 2006.
Emil M.
Constantinescu and Adrian Sandu, "Multirate timestepping
methods for hyperbolic conservation laws." Technical Report TR-06-15, Computer
Science, Virginia Tech, 2006.
GLM | IMEX | Multirate - [Example] | Publications - [Journals - Proceedings - Reports] | Related links | Top
| AMR's & frameworks [Links - Top] | ||
| Paramesh | [NEW] Version 4.0 (problems!!!) | |
| SciRun | current mesh infrastructure | |
| CHOMBO | [NEW] Version 2.0 | |
| CLAWPACK | finite volume framework | |
| Mathematical Software [Links - Top] | ||
| Mathematica | Mathematica (demos) and tutorials: basic and more advanced | |
| Numerical methods [Links - Top] | ||
| Willem Hundsdorfer's web page | ||
| http://math.la.asu.edu/~gardner/ENO.ps | ENO-WENO by C.-W. Shu | |
| Other [Links - Top] | ||
| Ellen W. Zegura's homepage | ||
| Visualization programs [Links - Top] | ||
| Vis5d | ||
| VTK | ||
| ParaView | ParaView is an open-source, multi-platform data analysis and visualization application. | |
| GGobi | GGobi is an open source visualization program for exploring high-dimensional data. | |
| Notes [Links - Top] | ||
| Lecture Notes On Discontinuous Galerkin Methods for convection-dominated problems | ||
| Height Coordinate Ocean Model | ||
| Sparse Matrix Compression Formats | ||
| Workaround [Links - Top] | ||
| SSH with MPI | ||
| Soft [Links - Top] | ||
| An Open-Source Finite Element Toolbox | ||
GLM | IMEX | Multirate - [Example] | Publications - [Journals - Proceedings - Reports] | Related links | Top