Binary Optimization via Stochastic Learning#
[7]:
from pyoed.optimization.binary_optimization import BinaryReinforceOptimizer
from pyoed.optimization.optimization_utils import pseudo_random_binary_objective_function
import matplotlib.pyplot as plt
[7]:
<function pyoed.optimization.optimization_utils.pseudo_random_binary_objective_function(x, scale=10.0, random_seed=1234)>
[2]:
def show_optimization_results(results):
"""Define a local function to plot optimization results given the ouput of optimizer `solve` method"""
# Show the Optimal Solution/Design
print(
f"Optimal Design: {results['optimal_design']}\n"
f"Optimal Objective Value: {results['optimal_design_objval']}"
)
# More details: show the Optimal policy (sampling probabilities)
print(
f"Optimal Plicy: {results['optimal_policy']}"
)
for i in range(len(results['optimal_policy_sample'])):
print(
f"Design Sample [{i+1}]: {results['optimal_policy_sample'][i]}; "
f" Objective = {results['optimal_policy_sample_objval'][i]}\n"
)
# Plot optimization trajectory
plt.plot(results['optimization_trajectory_stoch_objval'])
plt.xlabel('Optimization Iteration')
plt.ylabel('Objective')
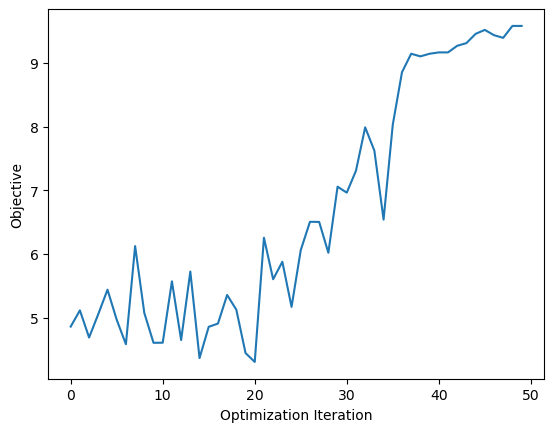
Maximization problem#
[3]:
# Create the optimizer & solve maximization problem (for a pseudo random function of binary variable)
# Size of the binary variable
problem_dimension = 10
optimizer = BinaryReinforceOptimizer(configs=configs)
[4]:
# Solve
maximization_results = optimizer.solve()
REINFORCE Iteration: 1 ; Step-Update-Norm: 0.08771353583025601
REINFORCE Iteration: 2 ; Step-Update-Norm: 0.1569671361454949
REINFORCE Iteration: 3 ; Step-Update-Norm: 0.17582391545796894
REINFORCE Iteration: 4 ; Step-Update-Norm: 0.1665119408836171
REINFORCE Iteration: 5 ; Step-Update-Norm: 0.21305932403935107
REINFORCE Iteration: 6 ; Step-Update-Norm: 0.21787447310878302
REINFORCE Iteration: 7 ; Step-Update-Norm: 0.18261770869935895
REINFORCE Iteration: 8 ; Step-Update-Norm: 0.21270444510646147
REINFORCE Iteration: 9 ; Step-Update-Norm: 0.16884242188120183
REINFORCE Iteration: 10 ; Step-Update-Norm: 0.15961792332519248
REINFORCE Iteration: 11 ; Step-Update-Norm: 0.2749639968767574
REINFORCE Iteration: 12 ; Step-Update-Norm: 0.1597535112241652
REINFORCE Iteration: 13 ; Step-Update-Norm: 0.2079692263537148
REINFORCE Iteration: 14 ; Step-Update-Norm: 0.11521492289358556
REINFORCE Iteration: 15 ; Step-Update-Norm: 0.2496512660692298
REINFORCE Iteration: 16 ; Step-Update-Norm: 0.13353600354819675
REINFORCE Iteration: 17 ; Step-Update-Norm: 0.15292817664611508
REINFORCE Iteration: 18 ; Step-Update-Norm: 0.18171468037411492
REINFORCE Iteration: 19 ; Step-Update-Norm: 0.19473484260542567
REINFORCE Iteration: 20 ; Step-Update-Norm: 0.2881915514863108
REINFORCE Iteration: 21 ; Step-Update-Norm: 0.09008580084731475
REINFORCE Iteration: 22 ; Step-Update-Norm: 0.18599815913710968
REINFORCE Iteration: 23 ; Step-Update-Norm: 0.06824307804150131
REINFORCE Iteration: 24 ; Step-Update-Norm: 0.09009126665971508
REINFORCE Iteration: 25 ; Step-Update-Norm: 0.1942482211223155
REINFORCE Iteration: 26 ; Step-Update-Norm: 0.1807684509617095
REINFORCE Iteration: 27 ; Step-Update-Norm: 0.1439670748238823
REINFORCE Iteration: 28 ; Step-Update-Norm: 0.16881584578389364
REINFORCE Iteration: 29 ; Step-Update-Norm: 0.11007496422693361
REINFORCE Iteration: 30 ; Step-Update-Norm: 0.15002503283707294
REINFORCE Iteration: 31 ; Step-Update-Norm: 0.2139690166804675
REINFORCE Iteration: 32 ; Step-Update-Norm: 0.15527826334172812
REINFORCE Iteration: 33 ; Step-Update-Norm: 0.23612546275574853
REINFORCE Iteration: 34 ; Step-Update-Norm: 0.57221173557408
REINFORCE Iteration: 35 ; Step-Update-Norm: 0.21955377156786382
REINFORCE Iteration: 36 ; Step-Update-Norm: 0.19960608453517115
REINFORCE Iteration: 37 ; Step-Update-Norm: 0.18367893400959065
REINFORCE Iteration: 38 ; Step-Update-Norm: 0.04273597041107824
REINFORCE Iteration: 39 ; Step-Update-Norm: 0.021829052860529274
REINFORCE Iteration: 40 ; Step-Update-Norm: 0.0047697929705715625
REINFORCE Iteration: 41 ; Step-Update-Norm: 0.030301332394224945
REINFORCE Iteration: 42 ; Step-Update-Norm: 0.17738310987947659
REINFORCE Iteration: 43 ; Step-Update-Norm: 0.09579783247649265
REINFORCE Iteration: 44 ; Step-Update-Norm: 0.16441388646649613
REINFORCE Iteration: 45 ; Step-Update-Norm: 0.24652070546046978
REINFORCE Iteration: 46 ; Step-Update-Norm: 0.1750256460085494
REINFORCE Iteration: 47 ; Step-Update-Norm: 0.005357326826412573
REINFORCE Iteration: 48 ; Step-Update-Norm: 0.19278726716429623
REINFORCE Iteration: 49 ; Step-Update-Norm: 0.0
[5]:
# Plot
show_optimization_results(maximization_results)
Optimal Design: [False True False True False False True True True True]
Optimal Objective Value: 9.581017261196408
Optimal Plicy: [0. 1. 0. 1. 0. 0. 1. 1. 1. 1.]
Design Sample [1]: [False True False True False False True True True True]; Objective = 9.581017261196408
Design Sample [2]: [False True False True False False True True True True]; Objective = 9.581017261196408
Design Sample [3]: [False True False True False False True True True True]; Objective = 9.581017261196408
Design Sample [4]: [False True False True False False True True True True]; Objective = 9.581017261196408
Design Sample [5]: [False True False True False False True True True True]; Objective = 9.581017261196408
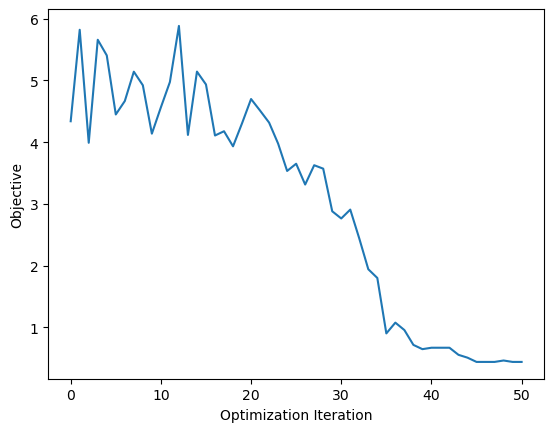
Minimization problem#
You can either recreate the optimizer with configuration maximize set to False, or simply update this configuration as follows
[6]:
# Set the optimization objective to minimization
optimizer.update_configurations(maximize=False)
# Solve & Plot
minimization_results = optimizer.solve()
show_optimization_results(minimization_results)
REINFORCE Iteration: 1 ; Step-Update-Norm: 0.12980145758387424
REINFORCE Iteration: 2 ; Step-Update-Norm: 0.12411385448768808
REINFORCE Iteration: 3 ; Step-Update-Norm: 0.16290915444186727
REINFORCE Iteration: 4 ; Step-Update-Norm: 0.10332665634439317
REINFORCE Iteration: 5 ; Step-Update-Norm: 0.16491986443338033
REINFORCE Iteration: 6 ; Step-Update-Norm: 0.1616742715529032
REINFORCE Iteration: 7 ; Step-Update-Norm: 0.14735495335802096
REINFORCE Iteration: 8 ; Step-Update-Norm: 0.2013415438724189
REINFORCE Iteration: 9 ; Step-Update-Norm: 0.11935329526047984
REINFORCE Iteration: 10 ; Step-Update-Norm: 0.12568219900040356
REINFORCE Iteration: 11 ; Step-Update-Norm: 0.19594375494188834
REINFORCE Iteration: 12 ; Step-Update-Norm: 0.10924429945851069
REINFORCE Iteration: 13 ; Step-Update-Norm: 0.16587667259653013
REINFORCE Iteration: 14 ; Step-Update-Norm: 0.12046232439210552
REINFORCE Iteration: 15 ; Step-Update-Norm: 0.19517457640972002
REINFORCE Iteration: 16 ; Step-Update-Norm: 0.15815680025605738
REINFORCE Iteration: 17 ; Step-Update-Norm: 0.19539179046502264
REINFORCE Iteration: 18 ; Step-Update-Norm: 0.22108676068236885
REINFORCE Iteration: 19 ; Step-Update-Norm: 0.29213075708847863
REINFORCE Iteration: 20 ; Step-Update-Norm: 0.11967646396169725
REINFORCE Iteration: 21 ; Step-Update-Norm: 0.1989239625553439
REINFORCE Iteration: 22 ; Step-Update-Norm: 0.12852077251599134
REINFORCE Iteration: 23 ; Step-Update-Norm: 0.13894608827889635
REINFORCE Iteration: 24 ; Step-Update-Norm: 0.1645257337423967
REINFORCE Iteration: 25 ; Step-Update-Norm: 0.25720421358502904
REINFORCE Iteration: 26 ; Step-Update-Norm: 0.09601470977549
REINFORCE Iteration: 27 ; Step-Update-Norm: 0.2402867983755446
REINFORCE Iteration: 28 ; Step-Update-Norm: 0.21761853441339596
REINFORCE Iteration: 29 ; Step-Update-Norm: 0.16618348229092927
REINFORCE Iteration: 30 ; Step-Update-Norm: 0.11023081651018224
REINFORCE Iteration: 31 ; Step-Update-Norm: 0.1969507951413673
REINFORCE Iteration: 32 ; Step-Update-Norm: 0.12042906885452338
REINFORCE Iteration: 33 ; Step-Update-Norm: 0.16498110477788389
REINFORCE Iteration: 34 ; Step-Update-Norm: 0.19849100286773166
REINFORCE Iteration: 35 ; Step-Update-Norm: 0.19073650676743248
REINFORCE Iteration: 36 ; Step-Update-Norm: 0.05296747213015411
REINFORCE Iteration: 37 ; Step-Update-Norm: 0.19763986158778846
REINFORCE Iteration: 38 ; Step-Update-Norm: 0.03404413752743814
REINFORCE Iteration: 39 ; Step-Update-Norm: 0.06498958639538166
REINFORCE Iteration: 40 ; Step-Update-Norm: 0.011482100411641216
REINFORCE Iteration: 41 ; Step-Update-Norm: 0.03470326261042311
REINFORCE Iteration: 42 ; Step-Update-Norm: 0.043288480878968305
REINFORCE Iteration: 43 ; Step-Update-Norm: 0.07451123943166027
REINFORCE Iteration: 44 ; Step-Update-Norm: 0.037537939299161716
REINFORCE Iteration: 45 ; Step-Update-Norm: 0.08485361654427825
REINFORCE Iteration: 46 ; Step-Update-Norm: 0.005937628880032908
REINFORCE Iteration: 47 ; Step-Update-Norm: 0.0014155945739890985
REINFORCE Iteration: 48 ; Step-Update-Norm: 0.00032107182972007653
REINFORCE Iteration: 49 ; Step-Update-Norm: 0.03021040839871736
REINFORCE Iteration: 50 ; Step-Update-Norm: 0.0
Optimal Design: [ True True True True False False False False True False]
Optimal Objective Value: 0.4426718163463439
Optimal Plicy: [1. 1. 1. 1. 0. 0. 0. 0. 1. 0.]
Design Sample [1]: [ True True True True False False False False True False]; Objective = 0.4426718163463439
Design Sample [2]: [ True True True True False False False False True False]; Objective = 0.4426718163463439
Design Sample [3]: [ True True True True False False False False True False]; Objective = 0.4426718163463439
Design Sample [4]: [ True True True True False False False False True False]; Objective = 0.4426718163463439
Design Sample [5]: [ True True True True False False False False True False]; Objective = 0.4426718163463439
[ ]:
