Algorithm for solving tridiagonal matrix problems in parallel

Abstract

A new algorithm is presented, designed to solve tridiagonal matrix problems efficiently with parallel computers (multiple instruction stream, multiple data stream (MIMD) machines with distributed memory). The algorithm is designed to be extendable to higher order banded diagonal systems.

I.  Introduction

1.

Factor the original matrix into a product of a block matrix (that can be divided up between processors) and a reduced matrix, which couples the block problems.

2.

Solve each block problem with one processor.

3.

Solve the reduced matrix problem.

Here, we propose a new approach to parallel solution of such systems. It is conceptually different from parallel factorization, in that the first step is avoided: no manipulations are performed on the original matrix before subdividing it among the processors. Avoiding this step has three advantages: simplicity, speed, and one less stability concern.

The method here is analogous to the solution of an inhomogeneous linear differential equation, where the solution is a ``particular'' solution added to an arbitrary linear combination of ``homogeneous'' solutions. The coefficients of the homogeneous solutions are later determined by boundary conditions. In our parallel method, each processor is given a contiguous subsection of a tridiagonal system. Even with no information about the neighboring subsystems, the solution can be obtained up to two constants. This completes the bulk of the necesary calculations. Once each processor has obtained such a solution, the global solution can be found by matching endpoints.

This approach allows a number of desirable features in both generality and efficient implementation. First, the method is readily generalizable to 5-diagonal and higher banded systems, as discussed in Sec VI. Second, the particular and homogeneous solutions can be calculated quite efficiently, since there are a number of overlapping calculations. Usual serial LU decomposition of a single M×M tridiagonal system requires 8M floating point operations and a temporary storage array of M elements [Press et al. or Hockney and Eastwood]. For the parallel routine below, the three solutions (one particular and two homogeneous) are calculated with 13M operations (not 3×8M = 24M) and no additional temporary storage arrays, while leaving the input data intact. Third, the interprocessor communication can be performed quite efficiently, by the all-to-all broadcast method described in Sec. IV. Finally, vector processors can be utilized effectively in cases where there are a number of banded diagonal systems to be solved.

This paper gives an implementation of this method. The algorithm is designed with the following objectives, listed in order of priority. First, the algorithm must minimize the number of interprocessor communications opened, since this is the most time consuming process. Second, the algorithm allows flexibility of the specific solution method of the tridiagonal submatrices. Here, we employ a variant of LU decomposition, but this is easily replaced with cyclic reduction or other. Third, we wish to minimize storage needs.

The remainder of this paper is organized as follows. Sec. II outlines the analysis underlying the routine. Sec. III describes an algorithm for computing the particular and two homogeneous routines in 13M operations. Sec. IV gives a method to assemble the reduced system efficiently in each processor, solve it, and complete the solution. Sec. V covers time consumption and performance of the algorithm. Sec. VI gives some conclusions and generalizations of this routine. The Appendix gives program segments.

II.  Basic Algorithm

Our algorithm is as follows. First, the linear system of order N is subdivided into P subsystems of order M. Thus, the N×N matrix Λ is divided into P submatrices L_p, each of dimension M×M,

Λ = |‾ | | | | | | | | |_ L1 c1MeMe1T a12e1eMT L2 cM2eMe1T . . . . . . . . cMP-1eMe1T a1Pe1eMT LP ‾| | | | | | | | | _| ,     (2-5)

where e_p is the p-th column of the M×M identity matrix. Similarly, the N dimensional vectors X and R are divided into P sub-vectors x and r, each of dimension M

X = |‾ |_ x1 x2 … xP ‾| _| T   , (2-6) R = |‾ |_ r1 r2 … rP ‾| _| T   . (2-7)

Here the submatrix L_p is given by

Lp = |‾ | | | | | | | | |_ BM(p-1)+1 CM(p-1)+1 AM(p-1)+2 BM(p-1)+2 CM(p-1)+2 . . . . . . . . CMp-1 AMp BMp ‾| | | | | | | | | _| ≡ |‾ | | | | | | | | |_ b1p c1p a2p b2p c2p . . . . . . . . cM-1p aMp bMp ‾| | | | | | | | | _| , (2-8)

for p = 1,2,…P, with similar and obvious definitions for x and r. For brevity, we have defined a_m^p ≡ A_M(p-1)+m, corresponding to the m^th subdiagonal element of the p^th submatrix. Similarly, b_m^p ≡ B_M(p-1)+m and c_m^p ≡ C_{M(p-1) +m}.

For each subsystem p we define three vectors x_p^R, x_p^UH, and x_p^LH as the solutions to the equations

Lp xpR ≡ rp, (2-9) Lp xpUH ≡ |‾ |_ -a1p 0 0 … 0 ‾| _| T   , (2-10) Lp xpLH ≡ |‾ |_ 0 0 0 … -cMp ‾| _| T   . (2-11)

The superscripts on the x stand for ``particular'' solution, ``upper homogeneous'' solution, and ``lower homogeneous'' solution respectively, from the inhomogeneous differential equation analogy.

The general solution of subsystem p consists of x_p^R added to an arbitrary linear combination of x_p^UH and x_p^LH,

xp = xpR + xpUHxpUH + xpLHxpLH,     (2-12)

where x_p^UH and x_p^LH are yet undetermined coefficients that depend on coupling to the neighboring solutions. To find x_p^UH and x^LH, Eq. (2-12) is substituted into Eq. (2-1). Straightforward calculation and various definitions in this section show that x₁^UH = x_P^LH = 0, and the remaining 2P-2 coefficients are determined by the solution to the following tridiagonal linear system, or "reduced" system

|‾ | | | | | | | | | | | | | | |_ x1,MLH -1 -1 x2,1UH x2,1LH x2,MUH x2,MLH -1 -1 x3,1UH x3,1LH x3,MUH x3,MLH -1 . . . . . . . . -1 -1 xP,1UH ‾| | | | | | | | | | | | | | | _| |‾ | | | | | | | | | | | | | | |_ x1LH x2UH x2LH x3UH x3LH . . xP-1LH xPUH ‾| | | | | | | | | | | | | | | _| = - |‾ | | | | | | | | | | | | | | |_ x1,MR x2,1R x2,MR x3,1R x3,MR . . xP-1,MR xP,MR ‾| | | | | | | | | | | | | | | _| ,     (2-13)

where x_p,m refers to the m^th element of the appropriate solution from the p^th submatrix.

The solution of Eq. (2-1), via subdivision and reassembly, is now complete. The outline of the algorithm is as follows:

1.

For each processor, find x_p^R, x_p^UH, and x_p^LH by solving Eqs. (2-9)-(2-11).

2.

Assemble the ``reduced'' system, Eq. (2-13), and solve for the x_p^UH and x_p^LH.

3.

For each processor, compute the final solution by Eq. (2-12).

III.  Computing the particular and homogeneous solutions

Equations (2-9)-(2-11) represent three M×M tridiagonal systems. If these systems were independent, then solution via LU decomposition would require 3×8M = 24M binary floating point operations. However, exploiting overlapping calculations and elements with value 0, gives the following algorithm, which can be implemented with 13M binary floating point operations.

Forward elimination: ω1 = c1 b1              ωi = ci bi-aiωi-1        i = 2,3,…M γ1 = r1 b1              γi = ri-aiγi-1 bi-aiωi-1        i = 2,3,…M Back substitution: xRM = γM              xRi = γi - ωi xRi+1       i = M-1,M-2,…1 xLHM = -ωM              xLHi = -ωi xLHi+1          i = M-1,M-2,…1 ωUHM = aM bM               ωUHi = ai bi-ciωi+1UH        i = M-1,M-2,…1 Forward substitution: xUH1 = -ω1UH               xUHi = -ωUHixUHi-1       i = 2,3,…M,

where the processor index p is implicitly present on all variables, and we have assumed that end elements a₁ and c_M are written in the appropriate positions in the a and c arrays. This algorithm is similar to the usual LU decomposition algorithm, (see, e.g., Press et al. or Hockney and Eastwod), but with an extra forward substitution. The sample FORTRAN segment in the Appendix implements this with no temporary storage arrays.

If the tridiagonal matrix is constant, and only the right hand side changes from one iteration to the next, then the vectors ω_i, 1/(b_i-a_iω_i), x^UH_i, and x^LH_i can be precalculated and stored. The computation then requires only 5M binary floating point operations.

IV.  Construction and solution of the reduced matrix

We assume that the following subroutines are available for interprocessor communication:

• Send(ToPid,data,n): When this is invoked by processor FromPid, the array data of length n is sent to processor ToPid. It is assumed that Send is nonblocking, in that the processor does not wait for the data to be received by ToPid before continuing.
• Receive(FromPid,data,n): To complete data transmission, Receive is invoked by processor ToPid. Upon execution, the array sent by processor FromPid is stored in the array data array of length n, It is assumed that Receive is blocking, in that the processor waits for the data to be received before continuing.

1. Each processor writes whatever data it has that is relevant to Eq. (2-13) in the array OutData.
2. The OutData arrays from each processor are concatenated as follows (Fig. 1):
   1. Each procesor p sends its OutData array to processor p-1 mod P, and receives a corresponding array from processor p+1 mod P, as depicted in Fig. 1a. The incoming array is concatenated to the end of OutData.
   2. At the i^th step, repeat the first step, except sending to processor p-2^i-1 mod P, and receiving from processor p+2^i-1 mod P (Fig. 1b,c), for i = 1,2,…. After log₂P iterations (or the next higher integer), each processor has the contents of the reduced matrix in the OutData array.
3. Each processor rearranges the contents of its OutData array into the reduced tridiagonal system, and then solves. (Each processor solves the same reduced system.)

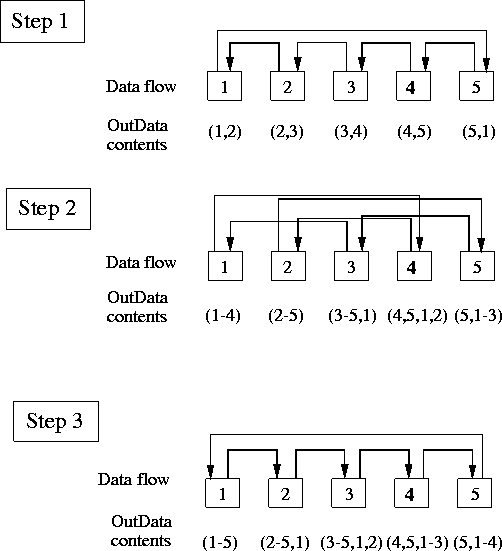
Figure 1.

Illustration of the method used to pass reduced matrix data between processors, with P = 5 for definiteness.

step 1:

In the first iteration, each processor p sends data to processor (p-1) mod P+1, receives data from processor (p+1) mod P+1, and concatenates the data arrays. The result is that each OutData array contains the data from the processors shown, in order shown. The remaining elements of the OutData array are not used.

step 2:

Each processor sends its OutData array to processor (p-2) mod P+1, receives data from processor (p+2) mod P+1, again concatenating.

step 3:

In the i^th iteration (here third and final), each processor sends its OutData array to processor (p-2^i-1) mod P+1, receives data from processor (p+2^i-1) mod P+1, again concatenating. The final OutData array contains all the information of the reduced matrix, ordered cyclically beginning with the contributions of the p^th processor. The information beyond the element Outdata(8P) is not used.

If the elements of the tridiagonal matrix are constants, then the reduced matrix can be precalculated and only the reduced right hand side needs to be assembled. In this case, the above routine could be rewritten to pass 1/4 as many real numbers. This does not represent a very large time savings, since generally it is the channel openings that is the most costly, not the amount of data passage.

At this point, the necessary components to Eq. (2-12) are stored in each processor. All that is left is the trivial task of picking out the correct coefficients and constructing the final solution. A sample program segment is provided in the Appendix.

V.  Performance

The time consumption for this routine is as follows.

1.

To calculate the three roots x^R, x^UH, and x^LH requires 13M binary floating point operations by each processor, done in parallel.

2.

To assemble the reduced matrix in each processor requires log₂P steps where interprocessor communications are opened, and the i^th opening passes 8×2^i-1 real numbers.

3.

Solution of the reduced system through LU decomposition requires 8(2P-2) binary floating point operations by each processor.

4.

Calculation of the final solution requires 4M binary floating point operations by each processor, done in parallel.

To test these claims empirically, the execution times of working serial and parallel codes were measured, and e_P was calculated both through its definition and through Eq. (5-2). Fig. 2 shows e_P as a function of P for two cases, N = 200 and N = 50,000. We conclude from Fig. 2 that Eq. (5-2) (smooth lines) is reasonably accurate, both for the theoretical maximum efficiency (47%, acheived for small P and large N) and for the scaling with large P.

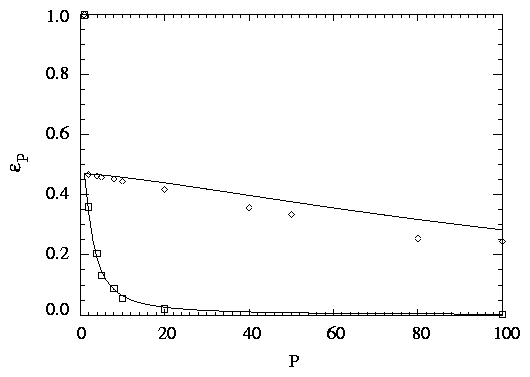
Figure 2.

Results of scaling runs, comparing the parallel time with serial LU decomposition time. Here, e_P is the parallel efficiency and P is the number of processors. The smooth lines represent Eq. (5-2), and the points are empirical results. The upper line and diamonds use N = 200, and the lower line and squares use N = 50,000.

It is difficult to make a comprehensive comparison with all other parallel tridiagonal solvers, but we can compare our speed with a popular algorithm by H. Wang. That routine requires 2P-2 steps where communications are opened (compared with log₂P such steps here), and 21M binary operations per processor (compared with 17M here). We have not performed empirical comparisons, but since both dominant processes have lower counts, it seems reasonable to believe the present algorithm is generally faster.

VI.  Discussion and Conclusions

Stability of this algorithm is similar to that of serial LU decomposition of a tridiagonal matrix. If the L_i are unstable to LU decomposition, then pivoting could be used. If the L_i are singular, then LU decomposition fails and some alternative should be devised. If the large matrix Λ is diagonally dominant, (|A_i| > |B_i|+|C_i|) then so too are the L_i. If the reduced system is unstable to LU decomposition, this can be replaced by a different solution scheme, with little loss of overall speed (if P << M).

This routine is generalizable from tridiagonal to higher systems. For example, in a 5-diagonal system, there would be four homogeneous solutions, each with an undetermined coefficient. The coefficients of the homogeneous solutions would be determined by a reduced system analogous to Eq. (2-13), except with O(4P) equations, not 2P-2.

We briefly discuss implementation of this routine in a problem where there are many tridiagonal systems to solve. This situation arises in many of the forseeable applications of parallel tridiagonal solvers, such as solving differential equations by the alternating-direction implicit method (ADI) (Press et al.) on a multidimensional grid. For definiteness we consider the two dimensional grid depicted in Fig. 3. For each grid line in y, there is a tridiagonal system to solve, with the index running in the x direction.

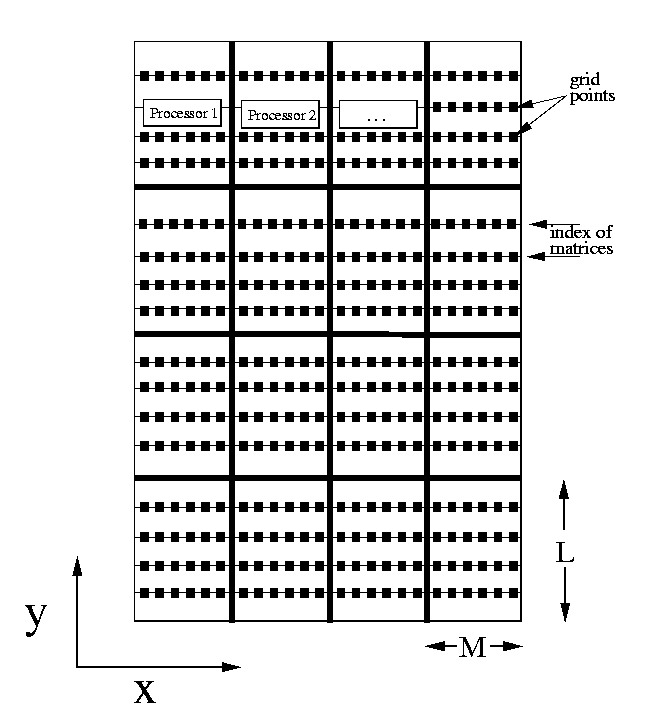
Figure 3.

Schematic representation of a typical set of tridiagonal systems that might arise in a two dimensional grid. For each grid line in y, there is a tridiagonal system to solve.

1.

The grid is divided into block subdomains in x and y. Each processor is assigned one subdomain, with the submatrices and sub-right hand sides stored locally. If the number of y grid lines in each subdomain is L, and the number of x grid points is M, then each processor has L systems with M equations each.

2.

Each processor finds x^R, x^UH, and x^LH, for each y grid line in its subdomain, by the algorithm described in Sec. III.

3.

To assemble the reduced systems, each family of processors colinear in x passes the reduced system data for all y grid lines in the subdomain, by the algorithm described in Sec. IV. (Note that the number of communication openings can be minimized by passing all L reduced systems together.) After this step is complete, each processor contains L reduced systems, one for each y grid line in its subdomain.

4.

Each processor solves the L reduced systems, then assembles the final solution, as described at the end of Sec. IV.

This work was performed for the U.S. Department of Energy at Lawrence Livermore National Laboratory under contract W7405-ENG-48.

Appendix

The particular and homogeneous solutions for each submatrix are computed by the algorithm in Sec. III. This is to be run by each processor, and it is assumed that the arrays a₁^p…a_M^p, b₁^p…b_M^p, c₁^p…c_M^p, and r₁^p…r_M^p are stored locally in each processor, with the index p omitted. No temporary arrays are needed; all intermediate storage is done in the final solution arrays, xr, xuh, and xlh (each with M elements).

!forward elimination:
  xuh(1) = c(1)/b(1)
  xlh(1) = r(1)/b(1)
  do i = 2,M,1
    denom = b(i) - c(i)*xuh(i-1)
    if (denom.eq.0) pause    !LU decomposition fails
    xuh(i) = c(i)/denom
    xlh(i) = (r(i) - a(i)*xlh(i-1))/denom
  end do


!back substitution:
  xr(M) = xlh(M)
  xlh(M) = -xuh(M)
  xuh(M) = a(M)/b(M)
  do i = M-1,1,-1
    xr(i) = xlh(i) - xuh(i)*xr(i+1)
    xlh(i) = -xuh(i)*xlh(i+1)
    denom = b(i) - c(i)*xuh(i+1)
    if (denom.eq.0) pause    !LU decomposition fails
   xuh(i) = -a(i)/denom
  end do


!forward substitution:
  xuh(1) = -xuh(1)
  do i = 2,M,1
    xuh(i) = -xuh(i)*xuh(i-1)
  end do

Sec. IV describes how the reduced matrix is written to each processor. A sample routine follows, to be executed by each processor. We assume the processors are numbered p = 1,2,…,P. The integer pid is the local processor number (called p in the mathematical parts of this paper), and the integer nprocs is the code name for P. The integer log2P is the smallest integer greater than or equal to log₂(P). The real array OutData has 8×2^log2P elements. The subroutine tridiagonal(a,b,c,r,sol,n) (not given here) is a serial subroutine that returns the solution sol for the tridiagonal system with subdiagonal a, diagonal b, superdiagonal c, and right hand side r, all of length n.

!write contributions of current processor into OutData:
  OutData(1) = -1. 
  OutData(2) = xuh(1)
  OutData(3) = xlh(1)
  OutData(4) = -xr(1)
  OutData(5) = xuh(M)
  OutData(6) = xlh(M)
  OutData(7) = -1.
  OutData(8) = -xr(M)


!concatenate all the OutData arrays:
  log2P = log(nprocs)/log(2)
  if (2**log2P.lt.nprocs) log2P = log2P+1 
  do i = 0,log2P-1,1
    nxfer = 8*(2**i)
    ToProc = 1 + mod(pid-2**i+2*nprocs,nprocs)
    FromProc = 1 + mod(pid+2**i,nprocs)
    call Send(ToProc,OutData,nxfer) 
    call Receive(FromProc,OutData(nxfer+1),nxfer)
  end do


!Put OutData into reduced tridiagonal form:
  nsig=8*nprocs               !no. of significant entries in OutData
  ifirst=8*(nprocs-pid) + 5   !index of a(1) in OutData
  do i = 1,2*nprocs-2,1 
    ibase = mod(ifirst+4*(i-1),nsig)
    reduca(i) = OutData(ibase)
    reducb(i) = OutData(ibase+1)
    reducc(i) = OutData(ibase+2)
    reducr(i) = OutData(ibase+3)
  end do


!solve reduced system:
 call tridiagonal(reduca,reducb,reducc,reducr,coeffs,2*nprocs-2) 

Once the reduced matrix is solved, then the solution can be assembled in each processor as follows.

!pick out the appropriate elements of coeffs:
  if (processor.ne.1) then 
    uhcoeff = coeffs(2*processor-2) 
  else
    uhcoeff = 0.
  end if
  if (processor.ne.nprocs) then 
    lhcoeff = coeffs(2*processor-1) 
  else
    lhcoeff = 0.
  end if


!compute the final solution:
  do i = 1,M,1
    x(i) = xr(i) + uhcoeff*xuh(i) + lhcoeff*xlh(i)
  end do

References

BBN Advanced Computers Inc., Inside the TC2000 Computer, Cambridge, MA, 25 (1989).

R. W. Hockney and J. W. Eastwood, Computer Simulation Using Particles, copyright 1988, Adam Hilger, Bristol, p. 185.

R. W. Hockney and C. R. Jesshope, Parallel Computers 2 (copyright 1988 by IOP Publishing, Ltd., Bristol).

C. E. Leith,``Domain Decomposition Message Passing for Diffusion and Fluid Flow,'' in The MPCI Yearly Report: The Attack of the Killer Micros, UCRL-ID-107022 (1991).

William H. Press, Brian P. Flannery, Saul A. Teukolsky, and William T. Vetterling, Numerical Recipes, copyright 1986, Cambridge University Press, pp. 19-40.

H. H. Wang, A parallel method for tridiagonal equations, ACM Trans. Math. Software 7:170-183 (1981).