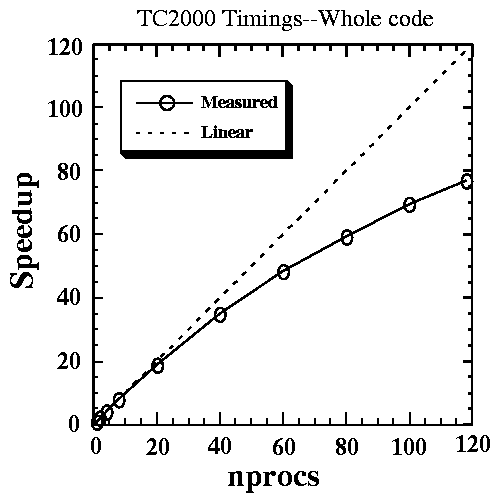
Figure 1: Measured speedups of whole simulation code on the TC2000 code. The short-dashed curve is the theoretical ideal linear speedup. Run parameters: 115351 particles, 32768 grid cells.
One of the grand challenge problems now supported by HPCC is the Numerical Tokamak Project. A goal of this project is the study of low-frequency microinstabilities in tokamak plasmas, which are believed to cause energy loss via turbulent thermal transport across the magnetic field lines. An important tool in this study is gyrokinetic particle-in-cell (PIC) simulation. Gyrokinetic, as opposed to fully-kinetic, methods are particularly well suited to the task because they are optimized to study the frequency and wavelength domain of the microinstabilities. Furthermore, many researchers now employ low-noise df methods (Dimits and Lee 1990, Kotschenreuther 1988) to greatly reduce statistical noise by modelling only the perturbation of the gyrokinetic distribution function from a fixed background, not the entire distribution function.
In spite of the increased efficiency of these improved algorithms over conventional PIC algorithms, gyrokinetic PIC simulations of tokamak microturbulence are still highly demanding of computer power-even fully-vectorized codes on vector supercomputers. For this reason, we have worked for several years to redevelop these codes on massively parallel computers. We have developed 3D gyrokinetic PIC simulation codes for SIMD and MIMD parallel processors, using control-parallel, data-parallel, and domain-decomposition message-passing (DDMP) programming paradigms. This poster summarizes our earlier work on codes for the Connection Machine and BBN TC2000, and our development of a generic DDMP code for distributed-memory parallel machines. We discuss the memory-access issues which are of key importance in writing parallel PIC codes, with special emphasis on issues peculiar to gyrokinetic PIC. We outline the domain decompositions in our new DDMP code and discuss the interplay of different domain decompositions suited for the particle-pushing and field-solution components of the PIC algorithm.
Particle-in-cell codes simulate plasmas using superparticles moving under self-consistent electromagnetic fields defined on a spatial grid; each superparticle represents many physical plasma particles. The (electromagnetic) force on each particle is computed by interpolating the electromagnetic fields from some set of neighboring points in the field grid. From these forces, accelerations are computed to update velocities, which in turn are applied to update the particle positions. Charge densities (and current densities, for non-electrostatic simulations) are then accumulated from the particle positions (and velocities) onto field grids, using an interpolation formula to compute each particle's contribution to a small set of nearby grid points. The field equations (Maxwell's equations) are then solved on the grid to yield updated electromagnetic fields; this closes the self-consistent loop, allowing computation of new forces to push the particles again, etc.
The basic ideas behind gyrokinetic PIC simulation (Lee 1987) are the
same as those behind conventional PIC simulation. Certain restrictions
are placed on the plasma behavior, however, to limit the range of
phenomena; most importantly, the fast gyroorbit motion perpendicular to
the magnetic field is eliminated (averaged out) by a formal
transformation of the kinetic equation which underlies the PIC method.
Formally, one assumes a gyrokinetic ordering of the system:
|
Computationally, the twist manifests itself in several ways: (1) The Poisson equation is modified by the inclusion of Bessel function terms which arise from gyroorbit averaging. (2) Only the guiding centers (centers of the gyroorbits) are followed, not the full particle orbits. To push the guiding center, a gyro-averaged force is computed by sampling the fields at several (typically 4) points separated by the Larmor radius from the guiding center. (3) Similarly, gyro-averaged charge/current densities are computed by accumulating at the several points on the gyroorbit and dividing the resulting density field by that number (the number of points).
In spite of the efficiency gained by not following ion cyclotron motion, more efficiency is needed in performing simulations on a transport timescale. We have expended much effort to use additional physics simplifications and algorithm improvements to reduce the computational cost of our vectorized Cray simulations. An example is the use of the δf method, in which the particles sample the perturbation of the phase-space distribution function away from a fixed background rather than the entire distribution function; this, when coupled with a partial linearization of the equations, can result in greatly reduced simulation noise-allowing the use of fewer particles (Dimits and Lee 1990, Kotschenreuther 1988).
The interpolation of forces from field-grid arrays to particle positions, and the complementary accumulation of densities from particle data to grid arrays are key elements of the PIC method. Another key element is the solution of the field equations, which are elliptic equations (boundary-value problems). Depending on the parallel programming paradigm used, these different elements present different types of problems for parallel simulation. Since the simulations we envision will have enough particles per cell that the field-solve will play a small role in the compute time, this paper will focus mainly on the key issues surrounding force interpolation and density accumulation.
The operation of reading field values from grid arrays to use with appropriate particle-array element for forcing is, computationally, a gather operation. The speed impediment in this operation on any type of computer, not just a parallel computer, is memory access speed. On a scalar workstation with a cache, for example, random hopping (particle-by-particle) through grid elements inhibits any benefit from data caching. On a vector processor, this random hopping inhibits fetches of large blocks of contiguous grid data into vectors. On a parallel processor, one has same problems as workstation and/or vector processor, plus the more severe problem of data communication: a grid element needed by a particle may be in a different processor's memory.
The operation of calculating data from particle array elements to accumulate into appropriate grid-array elements for charge/current accumulation is, computationally, a scatter with add. In addition to the memory-access problems of the gather operation, the scatter-add operation has an inherent data dependency: many particles may try to simultaneously accumulate into single grid cell if the particles are processed in parallel. This data dependency must be resolved on vector and parallel machines. Our C90 code uses the method of Heron and Adam (Heron and Adam 1989) to vectorize the charge accumulation, which requires storage of extra copies of the grid arrays. In the absence of sorting of the particle data, control parallel and data parallel codes must do something equivalent to employing hardware/software locks to protect the grid-array elements being updated. Sections 4.1 and 4.2 mention the negative impact this can have on performance.
With our production gyrokinetic PIC code on the Cray Research C90 machine at the National Energy Research Supercomputer Center, we have recently done a suite of runs to study the effect of shear in the E×B velocity on tokamak plasma microinstabilities. To do the runs, we use a 32×32×16 grid and 606797 particles (ions). To run long enough to get past the nonlinear saturation of the ITG instability we are modelling, we must run for at least 5000 timesteps (more for some velocity-shear parameters, since the shear reduces the growth rate of the instability).
The fully-vectorized code runs at 13.85 microseconds per particle per timestep on one processor of the C90, so a complete run takes at least 11.7 hours of CPU time. It is worth noting that our code, like all PIC codes, is limited by memory access speed rather than by floating-point operation speed. Measuring our code's speed with the CRI Hardware Performance Monitor (HPM) demonstrates this: The HPM reports 114 MFLOPS, 110 of which are vector operations, and an average vector length of 91.24; this shows that the code is well-vectorized. However, 114 MFLOPS is poor compared with the C90's peak speed of 1 GFLOPS; the disparity exists because the code is memory-access bound.
To simulate ITG instabilities in the regime of tokamak experimental parameters requires much larger runs than the runs discussed in the preceding section. In experiments, the density and temperature gradients are much weaker, and the ITG instabilities are much closer to the margin of instability. This demands more particles per grid cell and get adequate signal-to-noise ratio in the simulation. Furthermore, to simulate an adequate fraction of the tokamak's size and avoid simulation-box effects on the saturated turbulence demands a larger simulation grid. Yet furthermore, to actually achieve a physically realistic steady-state of saturated turbulence demands the inclusion of kinetic electrons and particle collisions , which were omitted in the aforementioned velocity-shear studies. Finally, to run such a simulation out long enough to study the desired transport timescale, rather than just the instability-saturation timescale, would require O(100-1000) times as many timesteps as in the velocity-shear studies. Using some parameters estimated in the Numerical Tokamak Proposal for a medium-to-large tokamak, such a simulation would require 2.8×104 CPU hours on the C90.
To put this last number in perspective, it is 3.2 years of C90 CPU time. This is too long. A run duration of O(10) CPU hours is tolerable, meaning we need a code/machine combination which is about 1000 times faster. This has led to the effort to use massively parallel processing in this project.
To be concrete, let control parallel be defined as a parallel programming paradigm in which one can dynamically or statically assign processors from a pool to various tasks such as loop iterates; serial program loops are parallelized using special loop syntax. As reported elsewhere (Williams and Matsuda 1992), we invested some time developing a control-parallel 3D gyrokinetic PIC code on the BBN TC2000 machine at LLNL (a 128-node MIMD machine with a butterfly-switch network). We employed the Parallel C Preprocessor and Parallel Fortran Preprocessor (PCP and PFP)(Brooks 1988, Gorda and Warren 1992); these are implementations of the split-join parallel programming paradigm, a statically-scheduled flavor of control parallelism.
The most scalable method for doing the charge accumulation in parallel proved to be a scheme using super-lightweight locks on a shared grid array. This accumulation (scatter-add), was the chief cause for loss of parallel efficiency, as shown in an earlier paper (Williams and Matsuda 1992) Figure 1 shows the scaling of the whole code with processor count; scalings of many individual algorithm components, such as the particle push, were closer to the linear ideal.
Figure 1: Measured speedups of whole simulation code on the TC2000 code. The short-dashed curve is the theoretical ideal linear speedup. Run parameters: 115351 particles, 32768 grid cells.
Let data parallel be defined as a parallel programming paradigm in which parallelism is achieved via parallel access of many elements in data arrays, and efficiency is gained by controlling the layout of data elements distributed across the processors. As reported elsewhere, we have developed a data-parallel 3D gyrokinetic PIC code on the CM2/200 machine at LANL (Williams and Matsuda 1992). We employed the CM Fortran data-parallel programming language, which is a sub/superset of Fortran 90.
In this code, the gathers for particle forcing and scatter-add's for charge accumulation are definite efficiency bottlenecks. They both require the most general, and slowest, kind of interprocessor communication functions. The communication for the gather (get) accounts for 30-45% of the total code execution time, and the communication for the scatter-add (send_add) accounts for 20-30% of the total code execution time (Williams and Byers 1992).
The following table summarizes some timing results for several runs using the vectorized C90 code, control-parallel TC2000 code, and data-parallel CM2/200 code; all runs used the δf algorithm. Run I is like the velocity-shear study parameters mentioned in section 3.1, with 16K grid cells and 606797 particles; Run II has 269001 particles and 16K grid cells. Runs on the TC2000 were run with 111 processors. The CM200 runs were done with 16K virtual processors (one quadrant); whole-machine CM200 timings have not been completed as of this writing. Scaling studies from one quadrant up to the whole machine with the older, non-δf code on the older CM2 machine showed nearly linear scaling (Williams and Matsuda 1992); since the CM200 differs only in clock speed, it is probably safe to assume that the full-machine CM200 run will be 4 times as fast as the one-quadrant run. Note that Run I is too large to fit in one quadrant, so timings for the CM200 are unavailable until full-machine runs can be done.
| 64-BIT FLOATING-POINT TIMINGS | ||
| (msec/particle/δt) | ||
| Run I | Run II | |
| C90 | 14msec | 15msec |
| TC2000 | 15msec | 20msec |
| CM200(16K) | N/A | 54msec |
Note that using 32-bit arithmetic, which is adequate for these simulations, on the TC2000 and CM200 results in codes that run O(1.5×) as fast.
While we have shown that these control-parallel and data-parallel codes on their respective parallel machines can compete with and even beat the Cray in performance, an interesting point, they have not provided the hundred or thousand-fold increase in speed we need to attack the desired problems described in the last part of section 3.2. This, and lessons learned from the experience of parallel programmers in other fields, has led to the creation of a new parallel code using a different parallel programming paradigm.
In the domain-decomposition message-passing (DDMP) paradigm, one decomposes the spatial simulation domain into subdomains; each processor used computes data on one subdomain. Subdomain border data is communicated with neighbor processors via explicit message passing function calls. The advantages of this paradigm are many: The ratio of communication to computation scales down with the ratio of subdomain surface to subdomain volume. The processors need only be loosely synchronized. The basic method is portable across many distributed-memory MIMD machines; all message-passing libraries provide the same basic send and receive capabilities. The method has disadvantages as well: Hand coding of the domain decomposition and buffering of messages is tedious. Intrinsically global data operations like solution of boundary-value problems may require lots of communication
The field grid arrays are decomposed into subdomains. Each processor only pushes the particles in its subdomain. Subdomain border data is sent to neighbor processors as messages; these take the form of grid data like accumulated charge density which spills over subdomain boundaries and particle data for particles which move across boundaries.
The gathers and scatters for the force computation and charge accumulation needn't be parallelized-each processor does them serially on only the data in its domain, which is stored in that processor's local memory. As the particles move across the subdomain boundaries, and their data is passed to neighboring processors in messages, there is the potential for load imbalance to develop because regions of high and low particle density appear. This load imbalance can be reduced or eliminated by dynamically revising the subdomains. For gyrokinetic PIC simulations this is not an extremely important issue, because the mathematical formulation precludes large nonuniformities in particle densities.
A problem faced by the DDMP programmer is difficulty in solving the field equations-for which FFT methods are typically used-on the domain-decomposed field-grid arrays.
Primary Domain Decomposition. A three-dimensional domain decomposition is employed for the field arrays. The number of processors is given as the product npx*npy*npz; there are, correspondingly, npx*npy*npz subdomains. Each subdomain spans ncx/npx grid cells in the x-direction, ncy/npy grid cells in the y-direction, and ncz/npz grid cells in the z-direction; where ncx is the number of grid cells in the x-dimension of the simulation box, etc.
Each processor processes only the particles in its subdomain. That processing includes charge accumulation and force computation. At each timestep, those particles which traverse subdomain boundaries are collected in buffers and sent with as messages to the appropriate neighbor processors. Figure 2 shows the primary domain decomposition.
Figure 2: 3D domain decomposition. Here npx ≡ the number of processors in the x-direction of this decompositon, etc.
To handle particle and grid operations near the subdomain boundaries, special extra cells called guard cells are employed. Figure 3 shows this schematically.
Figure 3: A subdomain. nsx ≡ number of grid cells in subdomain, ngx ≡ number of x-guard cells, Δx ≡ x-grid spacing, etc. The shaded region is the physical grid cells; the unshaded region is the guard cells.
Local Gathers And Scatters In the scatter-add part of the DDMP code, each processor accumulates from all the particles in its subdomain, then only the accumulated border grid data in the guard cells is sent to the appropriate neighbor processor. The number of items of data transferred is reduced by three heavy factors from the worst-case scenario of one data item per particle (as in data parallel codes): (1) the surface-to-volume ratio of the subdomains, (2) the number of particles per cell, and (3) the efficiency of bundling all the border grid data cells into a single buffer and sending only one message for each direction (all these sends for all directions happen at once, asynchronously, in all processors). Note that the in-processor accumulation could be vectorized using standard methods on a machine with vector nodes, and in-processor sorting of particle data could allow caching and reuse of contiguous blocks of local grid array elements.
In the gather part of the DDMP code, each processor needs only the grid data in its own local subdomain grid array to interpolate the force to all its particles' positions. For particles near the subdomain boundaries, the processor must access field grid data from the guard cells; this border grid data must have been received from the appropriate neighbor processor following the field equation solution. The same comments regarding efficiency of communication made above about the scatter-add apply to the communication required prior to the gather, as do the comments about caching of field-grid array elements.
The number of guard cells needed for a conventional PIC code is determined by the number of points in the interpolation formula used for accumulation and force interpolation. For the gyrokinetic code, the number of guard cells needed in plane perpendicular to the magnetic field is larger than this. The reason for this is that the gyrokinetic algorithm calls for sampling fields from some finite number of points on the particles' gyroorbits and averaging them to yield a force for the guiding center. Similarly, it calls for charge accumulation into points on the gyroorbit. These gyroorbit points are separated from the guiding center by the Larmor radius, which may be several grid cells in length.
Secondary Domain Decomposition For FFT. In order to formulate the 3D FFT as a collection of 1D FFT's which can be computed in parallel, three secondary domain decompositions are used. These are 2D, rather than 3D, decompositions; they break up the simulation domain blocks of 1D strips along each of the three directions.
The 3D FFT proceeds as follows: First, transform from the primary 3D domain decomposition (DD) to a 2D DD aligned along the x-dimension; this requires redistributing the grid data by passing blocks of data among the processors as messages. Each processor then owns a block of 1D x-strips whose length is the x-length of the simulation box. The processors all loop through their strips and perform 1D serial FFT's. Next, this 2D DD is transformed to a second 2D DD aligned with the y-dimension; the 1D y-dimension FFT's are then done in parallel as were the x-dimension FFT's. Next, this 2D DD is transformed to a third 2D DD aligned with the z-dimension, and the z-FFT's are done. Finally, this 2D DD is transformed back to the primary 3D DD. Figure 4 shows one of the secondary domain decompositions.
Figure 4: One of the three 2D domain decompositions used in the FFT for the field equation solve. This is decomposition #1, for transforming in the x-direction. Here npy1 ≡ the number of processors in the y-direction of this decompositon, etc.
Status. As of this writing, much of the writing of this new code is completed. Significant effort was lavished on the initialization routines: the reading of input parameters and broadcasting values to all processors is complete, as is initialization of periodicity tables and form-factor tables for the field solve. A simple version of the message-passing parallel FFT is nearly complete. A careful new particle-loading algorithm insures identical loading regardless of the number of processors or choice of domain decomposition.
Brooks, E. D. 1988. ``PCP: A Parallel Extension of C That is 99% Fat Free.'' UCRL-99673. Lawrence Livermore National Laboratory.
Dimits, A. M. and W. W. Lee. 1990. ``Partially Linearized Algorithms in Gyrokinetic Particle Simulations,'' PPPL-2718. Princeton Plasma Physics Laboratory (Oct.).
Gorda, B. C. and K. H. Warren 1992. ``PFP: A Scalable Parallel Programming Model.'' In The 1992 MPCI Yearly Report: Harnessing the Killer Micros, E. R. Brooks et. al. eds. Lawrence Livermore National Laboratory publication UCRL-ID-107022-92, 17-21.
Heron, A. and J. C. Adam. 1989. ``Particle Code Optimization on Vector Computers.'' J. Comput. Phys. 85 no. 2 (Dec.): 284-301.
Kotschenreuther, M. 1988. ``Numerical Simulation.'' Bull. Am. Phys. Soc. 34 no. 9 (Oct.): 2107.
Lee, W. W. 1987. ``Gyrokinetic Particle Simulation Model.'' J. Comput. Phys. 72 no. 1 (Sept.): 243-296.
Williams, T. J. and Y. Matsuda 1992. ``3D Gyrokinetic Particle-In-Cell Codes On The TC2000 And CM2.'' In The 1992 MPCI Yearly Report: Harnessing the Killer Micros, E. R. Brooks et. al. eds. Lawrence Livermore National Laboratory publication UCRL-ID-107022-92, 303-311.
Williams, T. J. and J. A. Byers. 1992. ``Memory Access in Massively Parallel Gyrokinetic PIC Simulations.'' Bull. Am. Phys. Soc. 37 no. 6 (Nov.): 1557.
1This work performed by LLNL under DoE contract No. W-7405-ENG-48.