Guide to the Stokes Equations using Finite Elements in PETSc

This guide accompanies SNES Example 62 and SNES Example 69.

The Stokes equations for a fluid, a steady-state form of the Navier-Stokes equations, start with the balance of momentum, just as in elastostatics,

\[\nabla \cdot \sigma + f = 0,\]

where \(\sigma\) is the stress tensor and \(f\) is the body force, combined with the conservation of mass

\[\nabla \cdot (\rho u) = 0,\]

where \(\rho\) is the density and \(u\) is the fluid velocity. If we assume that the density is constant, making the fluid incompressible, and that the rheology is Newtonian, meaning that the viscous stress is linearly proportional to the local strain rate, then we have

\[\begin{aligned} \nabla \cdot \mu \left( \nabla u + \nabla u^T \right) - \nabla p + f &= 0 \\ \nabla \cdot u &= 0 \end{aligned}\]

where \(p\) is the pressure, \(\mu\) is the dynamic shear viscosity, with units \(N\cdot s/m^2\) or \(Pa\cdot s\). If we divide by the constant density, we would have the kinematic viscosity \(\nu\) and a force per unit mass. The second equation demands that the velocity field be divergence-free, indicating that the flow is incompressible. The pressure in this case can be thought of as the Lagrange multiplier enforcing the incompressibility constraint. In the compressible case, we would need an equation of state to relate the pressure to the density, and perhaps temperature.

We will discretize our Stokes equations with finite elements, so the first step is to write a variational weak form of the equations. We choose to use a Ritz-Galerkin setup, so let our velocity \(u \in V\) and pressure \(p \in Q\), so that

\[\begin{aligned} \left< \nabla v, \mu \left( \nabla u + \nabla u^T \right) \right> + \left< v, \frac{\partial\sigma}{\partial n} \right>_\Gamma - \left< \nabla\cdot v, p \right> - \left< v, f \right> &= 0 & \text{for all} \ v \in V\\ \left< q, -\nabla \cdot u \right> &= 0 & \text{for all} \ q \in Q \end{aligned}\]

where integration by parts has added a boundary integral over the normal derivative of the stress (traction), and natural boundary conditions correspond to stress-free boundaries. We have multiplied the continuity equation by minus one in order to preserve symmetry.

Equation Definition

The test functions \(v, q\) and their derivatives are determined by the discretization, whereas the form of the integrand is determined by the physics. Given a quadrature rule to evaluate the form integral, we would only need the evaluation of the physics integrand at the quadrature points, given the values of the fields and their derivatives. The entire scheme is detailed in [KnepleyBrownRuppSmith13]. The kernels paired with test functions we will call \(f_0\) and those paired with gradients of test functions will be called \(f_1\).

For example, the kernel for the continuity equation, paired with the pressure test function, is called f0_p and can be seen here

static void f0_p(PetscInt dim, PetscInt Nf, PetscInt NfAux,
                 const PetscInt uOff[], const PetscInt uOff_x[], const PetscScalar u[], const PetscScalar u_t[], const PetscScalar u_x[],
                 const PetscInt aOff[], const PetscInt aOff_x[], const PetscScalar a[], const PetscScalar a_t[], const PetscScalar a_x[],
                 PetscReal t, const PetscReal x[], PetscInt numConstants, const PetscScalar constants[], PetscScalar f0[])
{
  PetscInt d;
  for (d = 0, f0[0] = 0.0; d < dim; ++d) f0[0] -= u_x[d*dim+d];
}

We use the components of the Jacobian of \(u\) to build up its divergence. For the balance of momentum excluding body force, we test against the gradient of the test function, as seen in f1_u,

static void f1_u(PetscInt dim, PetscInt Nf, PetscInt NfAux,
                 const PetscInt uOff[], const PetscInt uOff_x[], const PetscScalar u[], const PetscScalar u_t[], const PetscScalar u_x[],
                 const PetscInt aOff[], const PetscInt aOff_x[], const PetscScalar a[], const PetscScalar a_t[], const PetscScalar a_x[],
                 PetscReal t, const PetscReal x[], PetscInt numConstants, const PetscScalar constants[], PetscScalar f1[])
{
  const PetscReal mu = PetscRealPart(constants[0]);
  const PetscInt  Nc = uOff[1]-uOff[0];
  PetscInt        c, d;

  for (c = 0; c < Nc; ++c) {
    for (d = 0; d < dim; ++d) {
      f1[c*dim+d] = mu * (u_x[c*dim+d] + u_x[d*dim+c]);
    }

Notice how the pressure \(p\) is referred to using u[uOff[1]] so that we can have many fields with different numbers of components. DMPlex uses these point functions to construct the residual. A similar set of point functions is also used to build the Jacobian. The last piece of our physics specification is the construction of exact solutions using the Method of Manufactured Solutions (MMS).

MMS Solutions

An MMS solution is chosen to elucidate some property of the problem, and to check that it is being solved accurately, since the error can be calculated explicitly. For our Stokes problem, we first choose a solution with quadratic velocity and linear pressure,

\[u = \begin{pmatrix} x^2 + y^2 \\ 2 x^2 - 2 x y \end{pmatrix} \quad \mathrm{or} \quad \begin{pmatrix} 2 x^2 + y^2 + z^2 \\ 2 x^2 - 2xy \\ 2 x^2 - 2xz \end{pmatrix}\]

static PetscErrorCode quadratic_u(PetscInt dim, PetscReal time, const PetscReal x[], PetscInt Nc, PetscScalar *u, void *ctx)
{
  PetscInt c;

  u[0] = (dim-1)*PetscSqr(x[0]);
  for (c = 1; c < Nc; ++c) {
    u[0] += PetscSqr(x[c]);
    u[c]  = 2.0*PetscSqr(x[0]) - 2.0*x[0]*x[c];
  }
  return 0;
}

\[p = x + y - 1 \quad \mathrm{or} \quad x + y + z - \frac{3}{2}\]

static PetscErrorCode quadratic_p(PetscInt dim, PetscReal time, const PetscReal x[], PetscInt Nc, PetscScalar *u, void *ctx)
{
  PetscInt d;

  u[0] = -0.5*dim;
  for (d = 0; d < dim; ++d) u[0] += x[d];
  return 0;
}

By plugging these solutions into our equations, assuming that the velocity we choose is divergence-free, we can determine the body force necessary to make them satisfy the Stokes equations. For the quadratic solution above, we find

\[f = \begin{pmatrix} 1 - 4\mu \\ 1 - 4\mu \end{pmatrix} \quad \mathrm{or} \quad \begin{pmatrix} 1 - 8\mu \\ 1 - 4\mu \\ 1 - 4\mu \end{pmatrix}\]

which is implemented in our f0_quadratic_u pointwise function

static void f0_quadratic_u(PetscInt dim, PetscInt Nf, PetscInt NfAux,
                           const PetscInt uOff[], const PetscInt uOff_x[], const PetscScalar u[], const PetscScalar u_t[], const PetscScalar u_x[],
                           const PetscInt aOff[], const PetscInt aOff_x[], const PetscScalar a[], const PetscScalar a_t[], const PetscScalar a_x[],
                           PetscReal t, const PetscReal x[], PetscInt numConstants, const PetscScalar constants[], PetscScalar f0[])
{
  const PetscReal mu = PetscRealPart(constants[0]);
  PetscInt        d;

  f0[0] = (dim-1)*4.0*mu - 1.0;
  for (d = 1; d < dim; ++d) f0[d] = 4.0*mu - 1.0;
}

We let PETSc know about these solutions

  PetscCall(PetscDSSetExactSolution(ds, 0, exactFuncs[0], user));
  PetscCall(PetscDSSetExactSolution(ds, 1, exactFuncs[1], user));

These solutions will be captured exactly by the \(P_2-P_1\) finite element space. We can use the -dmsnes_check option to activate function space checks. It gives the \(L_2\) error, or discretization error, of the exact solution, the residual computed using the interpolation of the exact solution into our finite element space, and uses a Taylor test to check that our Jacobian matches the residual. It should converge at order 2, or be exact in the case of linear equations like Stokes. Our \(P_2-P_1\) runs in the PETSc test section at the bottom of the source file

    suffix: 2d_p2_p1_check
    requires: triangle
    args: -sol quadratic -vel_petscspace_degree 2 -pres_petscspace_degree 1 -dmsnes_check 0.0001

    suffix: 3d_p2_p1_check
    requires: ctetgen
    args: -sol quadratic -dm_plex_dim 3 -dm_plex_box_faces 2,2,2 -vel_petscspace_degree 2 -pres_petscspace_degree 1 -dmsnes_check 0.0001

verify these claims, as we can see from the output files

L_2 Error: [2.08577e-16, 3.51044e-17]
L_2 Residual: 3.30808e-15
Function appears to be linear

L_2 Error: [8.33588e-16, 9.09348e-17]
L_2 Residual: 2.40406e-15
Function appears to be linear

We can carry out the same tests for the \(Q_2-Q_1\) element,

    suffix: 2d_q2_q1_check
    args: -sol quadratic -dm_plex_simplex 0 -vel_petscspace_degree 2 -pres_petscspace_degree 1 -dmsnes_check 0.0001

    suffix: 3d_q2_q1_check
    args: -sol quadratic -dm_plex_simplex 0 -dm_plex_dim 3 -dm_plex_box_faces 2,2,2 -vel_petscspace_degree 2 -pres_petscspace_degree 1 -dmsnes_check 0.0001

The quadratic solution, however, cannot tell us whether our discretization is attaining the correct order of convergence, especially for higher order elements. Thus, we will define another solution based on trigonometric functions.

\[u = \begin{pmatrix} \sin(\pi x) + \sin(\pi y) \\ -\pi \cos(\pi x) y \end{pmatrix} \quad \mathrm{or} \quad \begin{pmatrix} 2 \sin(\pi x) + \sin(\pi y) + \sin(\pi z) \\ -\pi \cos(\pi x) y \\ -\pi \cos(\pi x) z \end{pmatrix}\]

static PetscErrorCode trig_u(PetscInt dim, PetscReal time, const PetscReal x[], PetscInt Nc, PetscScalar *u, void *ctx)
{
  PetscInt c;

  u[0] = (dim-1)*PetscSinReal(PETSC_PI*x[0]);
  for (c = 1; c < Nc; ++c) {
    u[0] += PetscSinReal(PETSC_PI*x[c]);
    u[c]  = -PETSC_PI*PetscCosReal(PETSC_PI*x[0]) * x[c];
  }
  return 0;
}

\[p = \sin(2 \pi x) + \sin(2 \pi y) \quad \mathrm{or} \quad \sin(2 \pi x) + \sin(2 \pi y) + \sin(2 \pi z)\]

static PetscErrorCode trig_p(PetscInt dim, PetscReal time, const PetscReal x[], PetscInt Nc, PetscScalar *u, void *ctx)
{
  PetscInt d;

  for (d = 0, u[0] = 0.0; d < dim; ++d) u[0] += PetscSinReal(2.0*PETSC_PI*x[d]);
  return 0;
}

\[f = \begin{pmatrix} 2 \pi \cos(2 \pi x) + \mu \pi^2 \sin(\pi x) + \mu \pi^2 \sin(\pi y) \\ 2 \pi \cos(2 \pi y) - \mu \pi^3 \cos(\pi x) y \end{pmatrix} \quad \mathrm{or} \quad \begin{pmatrix} 2 \pi \cos(2 \pi x) + 2\mu \pi^2 \sin(\pi x) + \mu \pi^2 \sin(\pi y) + \mu \pi^2 \sin(\pi z) \\ 2 \pi \cos(2 \pi y) - \mu \pi^3 cos(\pi x) y \\ 2 \pi \cos(2 \pi z) - \mu \pi^3 \cos(\pi x) z \end{pmatrix}\]

static void f0_quadratic_u(PetscInt dim, PetscInt Nf, PetscInt NfAux,
                           const PetscInt uOff[], const PetscInt uOff_x[], const PetscScalar u[], const PetscScalar u_t[], const PetscScalar u_x[],
                           const PetscInt aOff[], const PetscInt aOff_x[], const PetscScalar a[], const PetscScalar a_t[], const PetscScalar a_x[],
                           PetscReal t, const PetscReal x[], PetscInt numConstants, const PetscScalar constants[], PetscScalar f0[])
{
  const PetscReal mu = PetscRealPart(constants[0]);
  PetscInt        d;

  f0[0] = (dim-1)*4.0*mu - 1.0;
  for (d = 1; d < dim; ++d) f0[d] = 4.0*mu - 1.0;
}
}

We can now use -snes_convergence_estimate to determine the convergence exponent for the discretization. This options solves the problem on a series of refined meshes, calculates the error on each mesh, and determines the slope on a logarithmic scale. For example, we do this in two dimensions, refining our mesh twice using -convest_num_refine 2 in the following test.

    suffix: 2d_p2_p1_conv
    requires: triangle
    # Using -dm_refine 3 gives L_2 convergence rate: [3.0, 2.1]
    args: -sol trig -vel_petscspace_degree 2 -pres_petscspace_degree 1 -snes_convergence_estimate -convest_num_refine 2 -ksp_error_if_not_converged \
      -ksp_atol 1e-10 -ksp_error_if_not_converged -pc_use_amat \
      -pc_type fieldsplit -pc_fieldsplit_type schur -pc_fieldsplit_schur_fact_type full -pc_fieldsplit_schur_precondition a11 -pc_fieldsplit_off_diag_use_amat \
        -fieldsplit_velocity_pc_type lu -fieldsplit_pressure_ksp_rtol 1e-10 -fieldsplit_pressure_pc_type lu

However, the test needs an accurate linear solver. Sparse LU factorizations do not, in general, do full pivoting. Thus we must deal with the zero pressure block explicitly. We use the PCFIELDSPLIT preconditioner and the full Schur complement factorization, but we still need a preconditioner for the Schur complement \(B^T A^{-1} B\). We can have PETSc construct that matrix automatically, but the cost rises steeply as the problem size increases. Instead, we use the fact that the Schur complement is spectrally equivalent to the pressure mass matrix \(M_p\). We can make a preconditioning matrix, which has the diagonal blocks we will use to build the preconditioners, letting PETSc know that we get the off-diagonal blocks from the original system with -pc_fieldsplit_off_diag_use_amat and to build the Schur complement from the original matrix using -pc_use_amat,

  PetscCall(PetscDSSetJacobianPreconditioner(ds, 0, 0, NULL, NULL, NULL, g3_uu));
  PetscCall(PetscDSSetJacobianPreconditioner(ds, 1, 1, g0_pp, NULL, NULL, NULL));

Putting this all together, and using exact solvers on the subblocks, we have

    suffix: 2d_p2_p1_conv
    requires: triangle
    # Using -dm_refine 3 gives L_2 convergence rate: [3.0, 2.1]
    args: -sol trig -vel_petscspace_degree 2 -pres_petscspace_degree 1 -snes_convergence_estimate -convest_num_refine 2 -ksp_error_if_not_converged \
      -ksp_atol 1e-10 -ksp_error_if_not_converged -pc_use_amat \
      -pc_type fieldsplit -pc_fieldsplit_type schur -pc_fieldsplit_schur_fact_type full -pc_fieldsplit_schur_precondition a11 -pc_fieldsplit_off_diag_use_amat \
        -fieldsplit_velocity_pc_type lu -fieldsplit_pressure_ksp_rtol 1e-10 -fieldsplit_pressure_pc_type lu

and we see it converges, however it is superconverging in the pressure,

L_2 convergence rate: [2.6, 3.3]

If we refine the mesh using -dm_refine 3, the convergence rates become [3.0, 2.1].

Dealing with Parameters

Like most physical problems, the Stokes problem has a parameter, the dynamic shear viscosity, which determines what solution regime we are in. To handle these parameters in PETSc, we first define a C struct to hold them,

typedef struct {
  PetscScalar mu; /* dynamic shear viscosity */
} Parameter;

and then add a PetscBag object to our application context. We then setup the parameter object,

static PetscErrorCode SetupParameters(MPI_Comm comm, AppCtx *ctx)
{
  Parameter     *p;

  PetscFunctionBeginUser;
  /* setup PETSc parameter bag */
  PetscCall(PetscBagCreate(PETSC_COMM_SELF, sizeof(Parameter), &ctx->bag));
  PetscCall(PetscBagGetData(ctx->bag, (void **) &p));
  PetscCall(PetscBagSetName(ctx->bag, "par", "Stokes Parameters"));
  PetscCall(PetscBagRegisterScalar(ctx->bag, &p->mu, 1.0, "mu", "Dynamic Shear Viscosity, Pa s"));
  PetscCall(PetscBagSetFromOptions(ctx->bag));
  {
    PetscViewer       viewer;
    PetscViewerFormat format;
    PetscBool         flg;

    PetscCall(PetscOptionsGetViewer(comm, NULL, NULL, "-param_view", &viewer, &format, &flg));
    if (flg) {
      PetscCall(PetscViewerPushFormat(viewer, format));
      PetscCall(PetscBagView(ctx->bag, viewer));
      PetscCall(PetscViewerFlush(viewer));
      PetscCall(PetscViewerPopFormat(viewer));
      PetscCall(PetscViewerDestroy(&viewer));
    }
  }
  PetscFunctionReturn(0);
}

which will allow us to set the value from the command line using -mu. The PetscBag can also be persisted to disk with PetscBagLoad/View(). We can make these values available as constant to our pointwise functions through the PetscDS object.

  {
    Parameter  *param;
    PetscScalar constants[1];

    PetscCall(PetscBagGetData(user->bag, (void **) &param));
    constants[0] = param->mu; /* dynamic shear viscosity, Pa s */
    PetscCall(PetscDSSetConstants(ds, 1, constants));
  }

Investigating convergence

In order to look at the convergence of some harder problems, we will examine SNES ex69. This example provides an exact solution to the variable viscosity Stokes equation. The sharp viscosity variation will allow us to investigate convergence of the solver and discretization. Briefly, a sharp viscosity variation is created across the unit square, imposed on a background pressure with given fundamental frequency. For example, we can create examples with period one half and viscosity \(e^{2 B x}\) (solKx)

$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1" EXTRA_OPTIONS="-dm_refine 5 -dm_view hdf5:$PETSC_DIR/sol.h5 -snes_view_solution hdf5:$PETSC_DIR/sol.h5::append -exact_vec_view hdf5:$PETSC_DIR/sol.h5::append -m 2 -n 2 -B 1"
$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1" EXTRA_OPTIONS="-dm_refine 5 -dm_view hdf5:$PETSC_DIR/sol.h5 -snes_view_solution hdf5:$PETSC_DIR/sol.h5::append -exact_vec_view hdf5:$PETSC_DIR/sol.h5::append -m 2 -n 2 -B 3.75"

which are show in the figure below.

Fig. 10 Solution for \(m=2\), \(n=2\), \(B=1\)

Fig. 11 Solution for \(m=2\), \(n=2\), \(B=3.75\)

Debugging

If we can provide the PetscDS object in our problem with the exact solution function, PETSc has good support for debugging our discretization and solver. We can use the PetscConvEst object to check the convergence behavior of our element automatically. For example, if we use the -snes_convergence_estimate option, PETSc will solve our nonlinear equations on a series of refined meshes, use our exact solution to calculate the error, and then fit this line on a log-log scale to get the convergence rate,

    suffix: p2p1_conv
    requires: triangle
    # -dm_refine 2 gives L_2 convergence rate: [3.0, 2.2]
    args: -dm_plex_separate_marker -vel_petscspace_degree 2 -pres_petscspace_degree 1 \
      -snes_error_if_not_converged -snes_convergence_estimate -convest_num_refine 2 \
      -ksp_rtol 1.e-9 -ksp_error_if_not_converged -pc_use_amat \
      -pc_type fieldsplit -pc_fieldsplit_type schur -pc_fieldsplit_schur_factorization_type full -pc_fieldsplit_schur_precondition a11 \
        -fieldsplit_velocity_pc_type lu \
        -fieldsplit_pressure_ksp_rtol 1.e-9 -fieldsplit_pressure_pc_type lu

If we initially refine the mesh twice, -dm_refine 2, we get

L_2 convergence rate: [3.0, 2.2]

which are the convergence rates we expect for the velocity and pressure using a \(P_2-P_1\) discretization. For \(Q_1-P_0\)

    suffix: q1p0_conv
    # -dm_refine 2 gives L_2 convergence rate: [2.0, 1.0]
    args: -dm_plex_simplex 0 -dm_plex_separate_marker -vel_petscspace_degree 1 -pres_petscspace_degree 0 \
      -snes_error_if_not_converged -snes_convergence_estimate -convest_num_refine 2 \
      -ksp_rtol 1.e-9 -ksp_error_if_not_converged -pc_use_amat \
      -pc_type fieldsplit -pc_fieldsplit_type schur -pc_fieldsplit_schur_factorization_type full -pc_fieldsplit_schur_precondition a11 \
        -fieldsplit_velocity_pc_type lu \
        -fieldsplit_pressure_ksp_rtol 1.e-9 -fieldsplit_pressure_pc_type lu

we get

L_2 convergence rate: [2.0, 1.0]

This is a sensitive check that everything is working correctly. However, if this is wrong, where can I start? More fine-grained checks are available using the -dmsnes_check option. Using this for our \(P_2-P_1\) example (the p2p1 test), we have

L_2 Error: [0.000439127, 0.0376629]
L_2 Residual: 0.0453958
Function appears to be linear

The first line records the discretization error for our exact solution. This means that we project our solution function into the finite element space and then calculate the \(L_2\) norm of the difference between the exact solution and its projection. The norm is computed for each field separately. Next, PETSc calculates the residual using the projected exact solution as input. This should be small, and as the mesh is refined it should approach zero. Last, PETSc uses a Taylor test to try and determine how the error in the linear model scales as a function of the perturbation \(h\). Thus, in a nonlinear situation we would expect

Taylor approximation converging at order 2.0

In this case, since the viscosity does not depend on the velocity or pressure fields, we detect that the linear model is exact

Function appears to be linear

Suppose that we have made an error in the Jacobian. For instance, let us accidentally flip the sign of the pressure term in the momentum Jacobian.

static void stokes_momentum_pres_J(PetscInt dim, PetscInt Nf, PetscInt NfAux,
                                   const PetscInt uOff[], const PetscInt uOff_x[], const PetscScalar u[], const PetscScalar u_t[], const PetscScalar u_x[],
                                   const PetscInt aOff[], const PetscInt aOff_x[], const PetscScalar a[], const PetscScalar a_t[], const PetscScalar a_x[],
                                   PetscReal t, PetscReal u_tShift, const PetscReal x[], PetscInt numConstants, const PetscScalar constants[], PetscScalar g2[])
{
  PetscInt d;
  for (d = 0; d < dim; ++d) g2[d*dim+d] = -1.0; /* \frac{\partial\psi^{u_d}}{\partial x_d} */

When we run, we get a failure of the nonlinear solver. Our checking reveals that the Jacobian is wrong because it is converging at order 1 instead of 2, meaning the linear term is not correct in our model.

$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1" EXTRA_OPTIONS="-snes_monitor -ksp_monitor_true_residual -ksp_converged_reason"
L_2 Error: [0.000439127, 0.0376629]
L_2 Residual: 0.0453958
Taylor approximation converging at order 1.00
  0 SNES Function norm 1.170604545948e-01
    0 KSP preconditioned resid norm 4.965098891419e-01 true resid norm 1.170604545948e-01 ||r(i)||/||b|| 1.000000000000e+00
    1 KSP preconditioned resid norm 9.236805404733e-11 true resid norm 1.460082233654e-12 ||r(i)||/||b|| 1.247289051378e-11
  Linear solve converged due to CONVERGED_ATOL iterations 1
[0]PETSC ERROR: --------------------- Error Message --------------------------------------------------------------
[0]PETSC ERROR:
[0]PETSC ERROR: SNESSolve has not converged

In order to track down the error, we can use -snes_test_jacobian which computes a finite difference approximation to the Jacobian and compares that to the analytic Jacobian. We ignore the first test, which occurs during our testing of the Jacobian, and look at the test that happens during the first Newton iterate. We see that the relative error in the Frobenius norm is about one percent, which indicates we have a real problem.

$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1" EXTRA_OPTIONS="-snes_monitor -ksp_monitor_true_residual -ksp_converged_reason -snes_test_jacobian"
L_2 Error: [0.000439127, 0.0376629]
L_2 Residual: 0.0453958
  ---------- Testing Jacobian -------------
  Run with -snes_test_jacobian_view and optionally -snes_test_jacobian <threshold> to show difference
    of hand-coded and finite difference Jacobian entries greater than <threshold>.
  Testing hand-coded Jacobian, if (for double precision runs) ||J - Jfd||_F/||J||_F is
    O(1.e-8), the hand-coded Jacobian is probably correct.
  ||J - Jfd||_F/||J||_F = 136.793, ||J - Jfd||_F = 136.793
  ---------- Testing Jacobian for preconditioner -------------
  ||J - Jfd||_F/||J||_F = 136.793, ||J - Jfd||_F = 136.793
Taylor approximation converging at order 1.00
  0 SNES Function norm 1.170604545948e-01
  ---------- Testing Jacobian -------------
  ||J - Jfd||_F/||J||_F = 0.0119377, ||J - Jfd||_F = 1.63299
  ---------- Testing Jacobian for preconditioner -------------
  ||J - Jfd||_F/||J||_F = 0.008471, ||J - Jfd||_F = 1.15873
    0 KSP preconditioned resid norm 4.965098891419e-01 true resid norm 1.170604545948e-01 ||r(i)||/||b|| 1.000000000000e+00
    1 KSP preconditioned resid norm 9.236804064319e-11 true resid norm 1.460031196842e-12 ||r(i)||/||b|| 1.247245452699e-11
  Linear solve converged due to CONVERGED_ATOL iterations 1
[0]PETSC ERROR: --------------------- Error Message --------------------------------------------------------------
[0]PETSC ERROR:
[0]PETSC ERROR: SNESSolve has not converged

At this point, we could just go back and check the code. However, PETSc will also print out the differences between the analytic and approximate Jacobians. When we give the -snes_test_jacobian_view option, the code will print both Jacobians (which we omit) and then their difference, and will also do this for the preconditioning matrix (which we omit). It is clear from the output that the \(u-p\) block of the Jacobian is wrong, and thus we know right where to look for our error. Moreover, if we look at the values in row 15, we see that the values just differ by a sign.

$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1" EXTRA_OPTIONS="-snes_monitor -ksp_monitor_true_residual -ksp_converged_reason -snes_test_jacobian"
        Hand-coded minus finite-difference Jacobian with tolerance 1e-05 ----------
Mat Object: 1 MPI processes
  type: seqaij
row 0:
row 1:
row 2:
row 3:
row 4:
row 5:
row 6:
row 7:
row 8:
row 9:
row 10:
row 11:
row 12:
row 13:
row 14:
row 15: (0, 0.166667)  (2, -0.166667)
row 16: (0, 0.166667)  (2, -0.166667)  (5, 0.166667)  (8, -0.166667)
row 17: (0, 0.166667)  (2, 0.166667)  (5, -0.166667)  (8, -0.166667)
row 18: (0, 0.166667)  (5, -0.166667)
row 19: (5, 0.166667)  (8, -0.166667)  (11, 0.166667)  (13, -0.166667)
row 20: (5, 0.166667)  (8, 0.166667)  (11, -0.166667)  (13, -0.166667)
row 21: (5, 0.166667)  (11, -0.166667)
row 22: (5, 0.333333)  (8, -0.333333)
row 23: (2, 0.166667)  (5, 0.166667)  (8, -0.166667)  (11, -0.166667)
row 24: (2, 0.166667)  (3, -0.166667)  (5, 0.166667)  (8, -0.166667)
row 25: (2, 0.333333)  (8, -0.333333)
row 26: (2, 0.166667)  (3, -0.166667)  (8, 0.166667)  (10, -0.166667)
row 27: (2, 0.166667)  (3, 0.166667)  (8, -0.166667)  (10, -0.166667)
row 28: (3, 0.166667)  (10, -0.166667)
row 29: (8, 0.333333)  (10, -0.333333)
row 30: (3, 0.166667)  (8, 0.166667)  (10, -0.166667)  (13, -0.166667)
row 31: (2, 0.166667)  (3, -0.166667)
row 32: (8, 0.166667)  (10, -0.166667)  (13, 0.166667)  (14, -0.166667)
row 33: (8, 0.166667)  (10, 0.166667)  (13, -0.166667)  (14, -0.166667)
row 34: (10, 0.166667)  (14, -0.166667)
row 35: (13, 0.166667)  (14, -0.166667)
row 36: (8, 0.166667)  (10, -0.166667)  (11, 0.166667)  (13, -0.166667)
row 37: (8, 0.333333)  (13, -0.333333)
row 38: (11, 0.166667)  (13, -0.166667)
          0 KSP preconditioned resid norm 4.965098891419e-01 true resid norm 1.170604545948e-01 ||r(i)||/||b|| 1.000000000000e+00
          1 KSP preconditioned resid norm 9.236804067326e-11 true resid norm 1.460031196842e-12 ||r(i)||/||b|| 1.247245452699e-11
        Linear solve converged due to CONVERGED_ATOL iterations 1
      [0]PETSC ERROR: --------------------- Error Message --------------------------------------------------------------
      [0]PETSC ERROR:
      [0]PETSC ERROR: SNESSolve has not converged

Can we see that the Schur complement of Q1-P0 is ill-conditioned?

Optimizing the Solver

In order to see exactly what solver we have employed, we can use the -snes_view option. When checking \(P_2-P_1\) convergence, we use an exact solver, but it must have several parts in order to deal with the saddle-point in the Jacobian. Using the test system to provide our extra option, we get

$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1" EXTRA_OPTIONS="-snes_view"
SNES Object: 1 MPI processes
  type: newtonls
  maximum iterations=50, maximum function evaluations=10000
  tolerances: relative=1e-08, absolute=1e-50, solution=1e-08
  total number of linear solver iterations=1
  total number of function evaluations=2
  norm schedule ALWAYS
  SNESLineSearch Object: 1 MPI processes
    type: bt
      interpolation: cubic
      alpha=1.000000e-04
    maxstep=1.000000e+08, minlambda=1.000000e-12
    tolerances: relative=1.000000e-08, absolute=1.000000e-15, lambda=1.000000e-08
    maximum iterations=40
  KSP Object: 1 MPI processes
    type: gmres
      restart=30, using Classical (unmodified) Gram-Schmidt Orthogonalization with no iterative refinement
      happy breakdown tolerance 1e-30
    maximum iterations=10000, initial guess is zero
    tolerances:  relative=1e-09, absolute=1e-10, divergence=10000.
    left preconditioning
    using PRECONDITIONED norm type for convergence test
  PC Object: 1 MPI processes
    type: fieldsplit
      FieldSplit with Schur preconditioner, factorization FULL
      Preconditioner for the Schur complement formed from A11
      Split info:
      Split number 0 Defined by IS
      Split number 1 Defined by IS
      KSP solver for A00 block
        KSP Object: (fieldsplit_velocity_) 1 MPI processes
          type: gmres
            restart=30, using Classical (unmodified) Gram-Schmidt Orthogonalization with no iterative refinement
            happy breakdown tolerance 1e-30
          maximum iterations=10000, initial guess is zero
          tolerances:  relative=1e-05, absolute=1e-50, divergence=10000.
          left preconditioning
          using PRECONDITIONED norm type for convergence test
        PC Object: (fieldsplit_velocity_) 1 MPI processes
          type: lu
            out-of-place factorization
            tolerance for zero pivot 2.22045e-14
            matrix ordering: nd
            factor fill ratio given 5., needed 1.15761
              Factored matrix follows:
                Mat Object: 1 MPI processes
                  type: seqaij
                  rows=30, cols=30
                  package used to perform factorization: petsc
                  total: nonzeros=426, allocated nonzeros=426
                    using I-node routines: found 17 nodes, limit used is 5
          linear system matrix followed by preconditioner matrix:
          Mat Object: 1 MPI processes
            type: seqaij
            rows=30, cols=30
            total: nonzeros=368, allocated nonzeros=368
            total number of mallocs used during MatSetValues calls=0
              using I-node routines: found 20 nodes, limit used is 5
          Mat Object: (fieldsplit_velocity_) 1 MPI processes
            type: seqaij
            rows=30, cols=30
            total: nonzeros=368, allocated nonzeros=368
            total number of mallocs used during MatSetValues calls=0
              using I-node routines: found 20 nodes, limit used is 5
      KSP solver for S = A11 - A10 inv(A00) A01
        KSP Object: (fieldsplit_pressure_) 1 MPI processes
          type: gmres
            restart=30, using Classical (unmodified) Gram-Schmidt Orthogonalization with no iterative refinement
            happy breakdown tolerance 1e-30
          maximum iterations=10000, initial guess is zero
          tolerances:  relative=1e-09, absolute=1e-50, divergence=10000.
          left preconditioning
          using PRECONDITIONED norm type for convergence test
        PC Object: (fieldsplit_pressure_) 1 MPI processes
          type: lu
            out-of-place factorization
            tolerance for zero pivot 2.22045e-14
            matrix ordering: nd
            factor fill ratio given 5., needed 1.2439
              Factored matrix follows:
                Mat Object: 1 MPI processes
                  type: seqaij
                  rows=9, cols=9
                  package used to perform factorization: petsc
                  total: nonzeros=51, allocated nonzeros=51
                    not using I-node routines
          linear system matrix followed by preconditioner matrix:
          Mat Object: (fieldsplit_pressure_) 1 MPI processes
            type: schurcomplement
            rows=9, cols=9
              has attached null space
              Schur complement A11 - A10 inv(A00) A01
              A11
                Mat Object: 1 MPI processes
                  type: seqaij
                  rows=9, cols=9
                  total: nonzeros=41, allocated nonzeros=41
                  total number of mallocs used during MatSetValues calls=0
                    has attached null space
                    not using I-node routines
              A10
                Mat Object: 1 MPI processes
                  type: seqaij
                  rows=9, cols=30
                  total: nonzeros=122, allocated nonzeros=122
                  total number of mallocs used during MatSetValues calls=0
                    not using I-node routines
              KSP of A00
                KSP Object: (fieldsplit_velocity_) 1 MPI processes
                  type: gmres
                    restart=30, using Classical (unmodified) Gram-Schmidt Orthogonalization with no iterative refinement
                    happy breakdown tolerance 1e-30
                  maximum iterations=10000, initial guess is zero
                  tolerances:  relative=1e-05, absolute=1e-50, divergence=10000.
                  left preconditioning
                  using PRECONDITIONED norm type for convergence test
                PC Object: (fieldsplit_velocity_) 1 MPI processes
                  type: lu
                    out-of-place factorization
                    tolerance for zero pivot 2.22045e-14
                    matrix ordering: nd
                    factor fill ratio given 5., needed 1.15761
                      Factored matrix follows:
                        Mat Object: 1 MPI processes
                          type: seqaij
                          rows=30, cols=30
                          package used to perform factorization: petsc
                          total: nonzeros=426, allocated nonzeros=426
                            using I-node routines: found 17 nodes, limit used is 5
                  linear system matrix followed by preconditioner matrix:
                  Mat Object: 1 MPI processes
                    type: seqaij
                    rows=30, cols=30
                    total: nonzeros=368, allocated nonzeros=368
                    total number of mallocs used during MatSetValues calls=0
                      using I-node routines: found 20 nodes, limit used is 5
                  Mat Object: (fieldsplit_velocity_) 1 MPI processes
                    type: seqaij
                    rows=30, cols=30
                    total: nonzeros=368, allocated nonzeros=368
                    total number of mallocs used during MatSetValues calls=0
                      using I-node routines: found 20 nodes, limit used is 5
              A01
                Mat Object: 1 MPI processes
                  type: seqaij
                  rows=30, cols=9
                  total: nonzeros=122, allocated nonzeros=122
                  total number of mallocs used during MatSetValues calls=0
                    using I-node routines: found 20 nodes, limit used is 5
          Mat Object: (fieldsplit_pressure_) 1 MPI processes
            type: seqaij
            rows=9, cols=9
            total: nonzeros=41, allocated nonzeros=41
            total number of mallocs used during MatSetValues calls=0
              not using I-node routines
    linear system matrix followed by preconditioner matrix:
    Mat Object: 1 MPI processes
      type: seqaij
      rows=39, cols=39
      total: nonzeros=653, allocated nonzeros=653
      total number of mallocs used during MatSetValues calls=0
        has attached null space
        using I-node routines: found 24 nodes, limit used is 5
    Mat Object: (prec_) 1 MPI processes
      type: seqaij
      rows=39, cols=39
      total: nonzeros=653, allocated nonzeros=653
      total number of mallocs used during MatSetValues calls=0
        using I-node routines: found 24 nodes, limit used is 5

Going through this piece-by-piece, we can see all the parts of our solver. At the top level, we have a SNES using Newton’s method

$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1" EXTRA_OPTIONS="-snes_view"
SNES Object: 1 MPI processes
  type: newtonls
  maximum iterations=50, maximum function evaluations=10000
  tolerances: relative=1e-08, absolute=1e-50, solution=1e-08
  total number of linear solver iterations=1
  total number of function evaluations=2
  norm schedule ALWAYS
  SNESLineSearch Object: 1 MPI processes
    type: bt
      interpolation: cubic
      alpha=1.000000e-04
    maxstep=1.000000e+08, minlambda=1.000000e-12
    tolerances: relative=1.000000e-08, absolute=1.000000e-15, lambda=1.000000e-08
    maximum iterations=40

For each nonlinear step, we use KSPGMRES to solve the Newton equation, preconditioned by PCFIELDSPLIT. We split the problem into two blocks, with the split determined by our DM, and combine those blocks using a Schur complement. The Schur complement is faithful since we use the FULL factorization type.

$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1" EXTRA_OPTIONS="-snes_view"
  KSP Object: 1 MPI processes
    type: gmres
      restart=30, using Classical (unmodified) Gram-Schmidt Orthogonalization with no iterative refinement
      happy breakdown tolerance 1e-30
    maximum iterations=10000, initial guess is zero
    tolerances:  relative=1e-09, absolute=1e-10, divergence=10000.
    left preconditioning
    using PRECONDITIONED norm type for convergence test
  PC Object: 1 MPI processes
    type: fieldsplit
      FieldSplit with Schur preconditioner, factorization FULL
      Preconditioner for the Schur complement formed from A11
      Split info:
      Split number 0 Defined by IS
      Split number 1 Defined by IS

We form the preconditioner for the Schur complement from the (1,1) block of our preconditioning matrix, which we have set to be the viscosity-weighted mass matrix

static void stokes_identity_J_kx(PetscInt dim, PetscInt Nf, PetscInt NfAux,
                                 const PetscInt uOff[], const PetscInt uOff_x[], const PetscScalar u[], const PetscScalar u_t[], const PetscScalar u_x[],
                                 const PetscInt aOff[], const PetscInt aOff_x[], const PetscScalar a[], const PetscScalar a_t[], const PetscScalar a_x[],
                                 PetscReal t, PetscReal u_tShift, const PetscReal x[], PetscInt numConstants, const PetscScalar constants[], PetscScalar g0[])
{
  const PetscReal mu = PetscExpReal(2.0*PetscRealPart(constants[2])*x[0]);
  g0[0] = 1.0/mu;
}

static void stokes_identity_J_cx(PetscInt dim, PetscInt Nf, PetscInt NfAux,
                                 const PetscInt uOff[], const PetscInt uOff_x[], const PetscScalar u[], const PetscScalar u_t[], const PetscScalar u_x[],
                                 const PetscInt aOff[], const PetscInt aOff_x[], const PetscScalar a[], const PetscScalar a_t[], const PetscScalar a_x[],
                                 PetscReal t, PetscReal u_tShift, const PetscReal x[], PetscInt numConstants, const PetscScalar constants[], PetscScalar g0[])
{
  const PetscReal mu = x[0] < PetscRealPart(constants[4]) ? PetscRealPart(constants[2]) : PetscRealPart(constants[3]);
  g0[0] = 1.0/mu;
}

The solver for the first block, representing the velocity, is GMRES/LU. Note that the prefix is fieldsplit_velocity_, constructed automatically from the name of the field in our DM. Also note that there are two matrices, one from our original matrix, and one from our preconditioning matrix, but they are identical. In an optimized, scalable solver, this block would likely be solved by multigrid, but here we use LU for verification purposes.

$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1" EXTRA_OPTIONS="-snes_view"
      KSP solver for A00 block
        KSP Object: (fieldsplit_velocity_) 1 MPI processes
          type: gmres
            restart=30, using Classical (unmodified) Gram-Schmidt Orthogonalization with no iterative refinement
            happy breakdown tolerance 1e-30
          maximum iterations=10000, initial guess is zero
          tolerances:  relative=1e-05, absolute=1e-50, divergence=10000.
          left preconditioning
          using PRECONDITIONED norm type for convergence test
        PC Object: (fieldsplit_velocity_) 1 MPI processes
          type: lu
            out-of-place factorization
            tolerance for zero pivot 2.22045e-14
            matrix ordering: nd
            factor fill ratio given 5., needed 1.15761
              Factored matrix follows:
                Mat Object: 1 MPI processes
                  type: seqaij
                  rows=30, cols=30
                  package used to perform factorization: petsc
                  total: nonzeros=426, allocated nonzeros=426
                    using I-node routines: found 17 nodes, limit used is 5
          linear system matrix followed by preconditioner matrix:
          Mat Object: 1 MPI processes
            type: seqaij
            rows=30, cols=30
            total: nonzeros=368, allocated nonzeros=368
            total number of mallocs used during MatSetValues calls=0
              using I-node routines: found 20 nodes, limit used is 5
          Mat Object: (fieldsplit_velocity_) 1 MPI processes
            type: seqaij
            rows=30, cols=30
            total: nonzeros=368, allocated nonzeros=368
            total number of mallocs used during MatSetValues calls=0
              using I-node routines: found 20 nodes, limit used is 5

The solver for the second block, with prefix fieldsplit_pressure_, is also GMRES/LU, however we cannot factor the Schur complement operator since we never explicitly assemble it. Thus we assemble the viscosity-weighted mass matrix on the pressure space as an approximation. Notice that the Schur complement has the velocity solver embedded in it.

$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1" EXTRA_OPTIONS="-snes_view"
      KSP solver for S = A11 - A10 inv(A00) A01
        KSP Object: (fieldsplit_pressure_) 1 MPI processes
          type: gmres
            restart=30, using Classical (unmodified) Gram-Schmidt Orthogonalization with no iterative refinement
            happy breakdown tolerance 1e-30
          maximum iterations=10000, initial guess is zero
          tolerances:  relative=1e-09, absolute=1e-50, divergence=10000.
          left preconditioning
          using PRECONDITIONED norm type for convergence test
        PC Object: (fieldsplit_pressure_) 1 MPI processes
          type: lu
            out-of-place factorization
            tolerance for zero pivot 2.22045e-14
            matrix ordering: nd
            factor fill ratio given 5., needed 1.2439
              Factored matrix follows:
                Mat Object: 1 MPI processes
                  type: seqaij
                  rows=9, cols=9
                  package used to perform factorization: petsc
                  total: nonzeros=51, allocated nonzeros=51
                    not using I-node routines
          linear system matrix followed by preconditioner matrix:
          Mat Object: (fieldsplit_pressure_) 1 MPI processes
            type: schurcomplement
            rows=9, cols=9
              has attached null space
              Schur complement A11 - A10 inv(A00) A01
              A11
                Mat Object: 1 MPI processes
                  type: seqaij
                  rows=9, cols=9
                  total: nonzeros=41, allocated nonzeros=41
                  total number of mallocs used during MatSetValues calls=0
                    has attached null space
                    not using I-node routines
              A10
                Mat Object: 1 MPI processes
                  type: seqaij
                  rows=9, cols=30
                  total: nonzeros=122, allocated nonzeros=122
                  total number of mallocs used during MatSetValues calls=0
                    not using I-node routines
              KSP of A00
                KSP Object: (fieldsplit_velocity_) 1 MPI processes
                  type: gmres
                    restart=30, using Classical (unmodified) Gram-Schmidt Orthogonalization with no iterative refinement
                    happy breakdown tolerance 1e-30
                  maximum iterations=10000, initial guess is zero
                  tolerances:  relative=1e-05, absolute=1e-50, divergence=10000.
                  left preconditioning
                  using PRECONDITIONED norm type for convergence test
                PC Object: (fieldsplit_velocity_) 1 MPI processes
                  type: lu
                    out-of-place factorization
                    tolerance for zero pivot 2.22045e-14
                    matrix ordering: nd
                    factor fill ratio given 5., needed 1.15761
                      Factored matrix follows:
                        Mat Object: 1 MPI processes
                          type: seqaij
                          rows=30, cols=30
                          package used to perform factorization: petsc
                          total: nonzeros=426, allocated nonzeros=426
                            using I-node routines: found 17 nodes, limit used is 5
                  linear system matrix followed by preconditioner matrix:
                  Mat Object: 1 MPI processes
                    type: seqaij
                    rows=30, cols=30
                    total: nonzeros=368, allocated nonzeros=368
                    total number of mallocs used during MatSetValues calls=0
                      using I-node routines: found 20 nodes, limit used is 5
                  Mat Object: (fieldsplit_velocity_) 1 MPI processes
                    type: seqaij
                    rows=30, cols=30
                    total: nonzeros=368, allocated nonzeros=368
                    total number of mallocs used during MatSetValues calls=0
                      using I-node routines: found 20 nodes, limit used is 5
              A01
                Mat Object: 1 MPI processes
                  type: seqaij
                  rows=30, cols=9
                  total: nonzeros=122, allocated nonzeros=122
                  total number of mallocs used during MatSetValues calls=0
                    using I-node routines: found 20 nodes, limit used is 5
          Mat Object: (fieldsplit_pressure_) 1 MPI processes
            type: seqaij
            rows=9, cols=9
            total: nonzeros=41, allocated nonzeros=41
            total number of mallocs used during MatSetValues calls=0
              not using I-node routines

Finally, the SNES viewer reports the system matrix and preconditioning matrix

$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1" EXTRA_OPTIONS="-snes_view"
    linear system matrix followed by preconditioner matrix:
    Mat Object: 1 MPI processes
      type: seqaij
      rows=39, cols=39
      total: nonzeros=653, allocated nonzeros=653
      total number of mallocs used during MatSetValues calls=0
        has attached null space
        using I-node routines: found 24 nodes, limit used is 5
    Mat Object: (prec_) 1 MPI processes
      type: seqaij
      rows=39, cols=39
      total: nonzeros=653, allocated nonzeros=653
      total number of mallocs used during MatSetValues calls=0
        using I-node routines: found 24 nodes, limit used is 5

We see that they have the same nonzero pattern, even though the preconditioning matrix only contains the diagonal blocks. This is because zeros were inserted to define the nonzero structure. We can remove these nonzeros by telling the DM not to insert zero at preallocation time, and also telling the matrix itself to ignore the zeros from the assembly process.

$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1" EXTRA_OPTIONS="-snes_view -dm_preallocate_only -prec_mat_ignore_zero_entries"
    linear system matrix followed by preconditioner matrix:
    Mat Object: 1 MPI processes
      type: seqaij
      rows=39, cols=39
      total: nonzeros=653, allocated nonzeros=653
      total number of mallocs used during MatSetValues calls=0
        has attached null space
        using I-node routines: found 24 nodes, limit used is 5
    Mat Object: (prec_) 1 MPI processes
      type: seqaij
      rows=39, cols=39
      total: nonzeros=409, allocated nonzeros=653
      total number of mallocs used during MatSetValues calls=0
        using I-node routines: found 29 nodes, limit used is 5

We can see a sparsity portrait of the system and preconditioning matrices if the installation supports X-windows visualization

$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1" EXTRA_OPTIONS="-ksp_view_mat draw -prec_mat_view draw -draw_pause -1"
$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1" EXTRA_OPTIONS="-ksp_view_mat draw -prec_mat_view draw -draw_save $PETSC_DIR/mat.png"
$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1" EXTRA_OPTIONS="-dm_preallocate_only -mat_ignore_zero_entries -prec_mat_ignore_zero_entries -ksp_view_mat draw -prec_mat_view draw -draw_save $PETSC_DIR/mat_sparse.png"

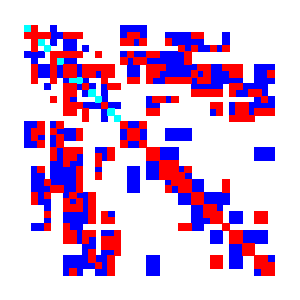
Fig. 12 System matrix	Fig. 13 System matrix with sparse stencil
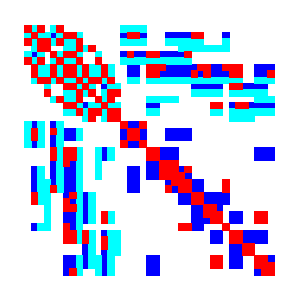
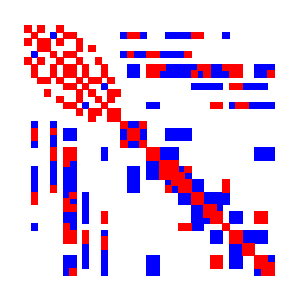
Fig. 14 Preconditioning matrix	Fig. 15 Preconditioning matrix with sparse stencil

If we want to check the convergence of the solver, we can also do that using options. Both the linear and nonlinear solvers converge in a single iteration, which is exactly what we want. In order to have this happen, we must have the tolerance on both the outer KSP solver and the inner Schur complement solver be low enough. Notice that the sure complement solver is used twice, and converges in seven iterates each time.

$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1" EXTRA_OPTIONS="-snes_monitor -ksp_monitor_true_residual -ksp_converged_reason -fieldsplit_pressure_ksp_converged_reason"
0 SNES Function norm 1.170604545948e-01
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 7
  0 KSP preconditioned resid norm 4.965098891419e-01 true resid norm 1.170604545948e-01 ||r(i)||/||b|| 1.000000000000e+00
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 7
  1 KSP preconditioned resid norm 9.236813926190e-11 true resid norm 1.460072673561e-12 ||r(i)||/||b|| 1.247280884579e-11
Linear solve converged due to CONVERGED_ATOL iterations 1
1 SNES Function norm 1.460070661322e-12

We can look at the scalability of the solve by refining the mesh. We see that the Schur complement solve looks robust to grid refinement.

$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1" EXTRA_OPTIONS="-dm_refine 2 -snes_monitor -ksp_monitor_true_residual -ksp_converged_reason -fieldsplit_pressure_ksp_converged_reason"
0 SNES Function norm 3.503062983054e-02
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 8
  0 KSP preconditioned resid norm 9.943095979973e-01 true resid norm 3.503062983054e-02 ||r(i)||/||b|| 1.000000000000e+00
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 8
  1 KSP preconditioned resid norm 1.148772629230e-10 true resid norm 2.693482255004e-13 ||r(i)||/||b|| 7.688934706664e-12
Linear solve converged due to CONVERGED_RTOL iterations 1
1 SNES Function norm 2.693649920420e-13
$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1" EXTRA_OPTIONS="-dm_refine 4 -snes_monitor -ksp_monitor_true_residual -ksp_converged_reason -fieldsplit_pressure_ksp_converged_reason"
0 SNES Function norm 8.969202737759e-03
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 6
  0 KSP preconditioned resid norm 3.322375727167e+00 true resid norm 8.969202737759e-03 ||r(i)||/||b|| 1.000000000000e+00
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 6
  1 KSP preconditioned resid norm 6.112282404006e-10 true resid norm 8.543800889926e-14 ||r(i)||/||b|| 9.525708292843e-12
Linear solve converged due to CONVERGED_RTOL iterations 1
1 SNES Function norm 8.543893996362e-14

Starting off with an exact solver allows us to check that the discretization, equations, and boundary conditions are correct. Moreover, choosing the Schur complement formulation, rather than a sparse direct solve, gives us a path to incremental boost the scalability. Our first step will be to replace the direct solve of the momentum operator, which has cost superlinear in \(N\), with a more scalable alternative. Since the operator is still elliptic, despite the viscosity variation, we should be able to use some form of multigrid. We will start with algebraic multigrid because it handles coefficient variation well, even if the setup time is larger than the geometric variant.

$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1" EXTRA_OPTIONS="-dm_refine 2 -snes_monitor -ksp_monitor_true_residual -ksp_converged_reason -fieldsplit_pressure_ksp_converged_reason -fieldsplit_velocity_pc_type gamg -fieldsplit_velocity_ksp_converged_reason"
0 SNES Function norm 3.503062983054e-02
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 8
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 9
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 9
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 9
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 10
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 9
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 9
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 8
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 8
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 8
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 9
  0 KSP preconditioned resid norm 9.943097452179e-01 true resid norm 3.503062983054e-02 ||r(i)||/||b|| 1.000000000000e+00
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 8
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 9
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 9
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 9
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 10
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 9
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 9
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 8
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 8
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 8
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 9
  1 KSP preconditioned resid norm 1.503326145261e-05 true resid norm 1.089276827085e-06 ||r(i)||/||b|| 3.109498265814e-05
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 10
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 9
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 9
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 9
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 9
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 9
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 9
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 9
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 9
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 9
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 9
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 10
  2 KSP preconditioned resid norm 1.353007845554e-10 true resid norm 6.056095141823e-11 ||r(i)||/||b|| 1.728799959098e-09
Linear solve converged due to CONVERGED_RTOL iterations 2
1 SNES Function norm 6.056096909907e-11

This looks alright, but the number of iterates grows with refinement. At 3 refinements, it is 16, 30 at 4 refinements, and 70 at 5 refinements. Increasing the number of smoother iterates to four, -fieldsplit_velocity_mg_levels_ksp_max_it 4, brings down the number of iterates, but not the growth. Using w-cycles and full multigrid does not help either. It is likely that the coarse grids made by MIS are inaccurate for the \(P_2\) discretization.

We can instead use geometric multigrid, and we would hope get more accurate coarse bases. The -dm_refine_hierarchy allows us to make a hierarchy of refined meshes and sets the number of multigrid levels automatically. Then all we need to specify is -fieldsplit_velocity_pc_type mg, as we see in the test

    suffix: p2p1_gmg
    requires: triangle
    args: -dm_plex_separate_marker -dm_refine_hierarchy 2 -vel_petscspace_degree 2 -pres_petscspace_degree 1 \
      -snes_error_if_not_converged -dmsnes_check .001 \
      -ksp_type fgmres -ksp_rtol 1.e-9 -ksp_error_if_not_converged -pc_use_amat \
      -pc_type fieldsplit -pc_fieldsplit_type schur -pc_fieldsplit_schur_factorization_type full -pc_fieldsplit_schur_precondition a11 \
        -fieldsplit_velocity_pc_type mg \
        -fieldsplit_pressure_ksp_rtol 1.e-9 -fieldsplit_pressure_pc_type lu

This behaves well for the initial mesh,

$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1_gmg" EXTRA_OPTIONS="-dm_refine_hierarchy 2 -snes_monitor -ksp_monitor_true_residual -ksp_converged_reason -fieldsplit_pressure_ksp_converged_reason -fieldsplit_velocity_ksp_converged_reason"
0 SNES Function norm 3.503062983054e-02
  0 KSP unpreconditioned resid norm 3.503062983054e-02 true resid norm 3.503062983054e-02 ||r(i)||/||b|| 1.000000000000e+00
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 5
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 5
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 8
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  1 KSP unpreconditioned resid norm 4.643855168829e-06 true resid norm 4.643855168807e-06 ||r(i)||/||b|| 1.325655630878e-04
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 5
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 5
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 5
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 9
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 5
  2 KSP unpreconditioned resid norm 1.520240889941e-11 true resid norm 1.520239396618e-11 ||r(i)||/||b|| 4.339743258890e-10
Linear solve converged due to CONVERGED_ATOL iterations 2
1 SNES Function norm 1.520237877998e-11

and is also stable under refinement

$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1_gmg" EXTRA_OPTIONS="-dm_refine_hierarchy 4 -snes_monitor -ksp_monitor_true_residual -ksp_converged_reason -fieldsplit_pressure_ksp_converged_reason -fieldsplit_velocity_ksp_converged_reason"
0 SNES Function norm 3.503062983054e-02
  0 KSP unpreconditioned resid norm 3.503062983054e-02 true resid norm 3.503062983054e-02 ||r(i)||/||b|| 1.000000000000e+00
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 5
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 5
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 8
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  1 KSP unpreconditioned resid norm 4.643855168829e-06 true resid norm 4.643855168807e-06 ||r(i)||/||b|| 1.325655630878e-04
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 5
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 5
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 4
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 5
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 9
  Linear fieldsplit_velocity_ solve converged due to CONVERGED_RTOL iterations 5
  2 KSP unpreconditioned resid norm 1.520240889941e-11 true resid norm 1.520239396618e-11 ||r(i)||/||b|| 4.339743258890e-10
Linear solve converged due to CONVERGED_ATOL iterations 2
1 SNES Function norm 1.520237877998e-11

Finally, we can back off the pressure solve. ILU(0) is good enough to maintain a constant number of iterates as we refine the grid. We could continue to refine our preconditioner by playing with the tolerance of the inner multigrid and Schur complement solves, trading fewer inner iterates for more outer iterates.

$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1_gmg" EXTRA_OPTIONS="-dm_refine_hierarchy 2 -snes_monitor -ksp_monitor_true_residual -ksp_converged_reason -fieldsplit_pressure_ksp_converged_reason -fieldsplit_pressure_pc_type ilu"
0 SNES Function norm 3.503062983054e-02
  0 KSP unpreconditioned resid norm 3.503062983054e-02 true resid norm 3.503062983054e-02 ||r(i)||/||b|| 1.000000000000e+00
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 10
  1 KSP unpreconditioned resid norm 4.643855785779e-06 true resid norm 4.643855785812e-06 ||r(i)||/||b|| 1.325655807011e-04
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 10
  2 KSP unpreconditioned resid norm 1.521944777036e-11 true resid norm 1.521942998859e-11 ||r(i)||/||b|| 4.344606437913e-10
Linear solve converged due to CONVERGED_ATOL iterations 2
1 SNES Function norm 1.521943449163e-11
$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1_gmg" EXTRA_OPTIONS="-dm_refine_hierarchy 4 -snes_monitor -ksp_monitor_true_residual -ksp_converged_reason -fieldsplit_pressure_ksp_converged_reason -fieldsplit_pressure_pc_type ilu"
0 SNES Function norm 8.969202737759e-03
  0 KSP unpreconditioned resid norm 8.969202737759e-03 true resid norm 8.969202737759e-03 ||r(i)||/||b|| 1.000000000000e+00
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 10
  1 KSP unpreconditioned resid norm 2.234849111673e-05 true resid norm 2.234849111674e-05 ||r(i)||/||b|| 2.491692045566e-03
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 10
  2 KSP unpreconditioned resid norm 1.205594722917e-10 true resid norm 1.205594316079e-10 ||r(i)||/||b|| 1.344148807121e-08
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 10
  3 KSP unpreconditioned resid norm 1.461086575333e-15 true resid norm 2.284323415523e-15 ||r(i)||/||b|| 2.546852247977e-13
Linear solve converged due to CONVERGED_ATOL iterations 3
1 SNES Function norm 2.317901194143e-15
$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1_gmg" EXTRA_OPTIONS="-dm_refine_hierarchy 6 -snes_monitor -ksp_monitor_true_residual -ksp_converged_reason -fieldsplit_pressure_ksp_converged_reason -fieldsplit_pressure_pc_type ilu"
0 SNES Function norm 2.252260693635e-03
  0 KSP unpreconditioned resid norm 2.252260693635e-03 true resid norm 2.252260693635e-03 ||r(i)||/||b|| 1.000000000000e+00
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 9
  1 KSP unpreconditioned resid norm 1.220195757583e-05 true resid norm 1.220195757579e-05 ||r(i)||/||b|| 5.417648858445e-03
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 10
  2 KSP unpreconditioned resid norm 2.683367607036e-09 true resid norm 2.683367591382e-09 ||r(i)||/||b|| 1.191410745197e-06
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 10
  3 KSP unpreconditioned resid norm 5.510932827474e-13 true resid norm 5.511665167379e-13 ||r(i)||/||b|| 2.447170162386e-10
Linear solve converged due to CONVERGED_ATOL iterations 3
1 SNES Function norm 5.511916500930e-13

We can make the problem harder by increasing the wave number and size of the viscosity perturbation. If we set the \(B\) parameter to 6.9, we have a factor of one million increase in viscosity across the cell. At this scale, we see that we lose enough accuracy in our Jacobian calculation to defeat our Taylor test, but we are still able to solve the problem efficiently.

$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1_gmg" EXTRA_OPTIONS="-dm_refine_hierarchy 2 -snes_monitor -ksp_monitor_true_residual -ksp_converged_reason -fieldsplit_pressure_ksp_converged_reason -fieldsplit_pressure_pc_type ilu -m 2 -n 2 -B 6.9"
L_2 Error: [4.07817e-06, 0.0104694]
L_2 Residual: 0.0145403
Taylor approximation converging at order 1.00
0 SNES Function norm 3.421266970274e-02
  0 KSP unpreconditioned resid norm 3.421266970274e-02 true resid norm 3.421266970274e-02 ||r(i)||/||b|| 1.000000000000e+00
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 21
  1 KSP unpreconditioned resid norm 2.066264276201e-05 true resid norm 2.066264276201e-05 ||r(i)||/||b|| 6.039471032675e-04
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 20
  2 KSP unpreconditioned resid norm 1.295461366009e-10 true resid norm 1.295461419342e-10 ||r(i)||/||b|| 3.786496144842e-09
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 20
  3 KSP unpreconditioned resid norm 1.954355290546e-15 true resid norm 1.954135246291e-15 ||r(i)||/||b|| 5.711729786858e-14
Linear solve converged due to CONVERGED_ATOL iterations 3
1 SNES Function norm 1.946196473520e-15
$ make -f ./gmakefile test globsearch="snes_tutorials-ex69_p2p1_gmg" EXTRA_OPTIONS="-dm_refine_hierarchy 6 -snes_monitor -ksp_monitor_true_residual -ksp_converged_reason -fieldsplit_pressure_ksp_converged_reason -fieldsplit_pressure_pc_type ilu -m 2 -n 2 -B 6.9"
L_2 Error: [1.52905e-09, 4.72606e-05]
L_2 Residual: 7.18836e-06
Taylor approximation converging at order 1.00
0 SNES Function norm 2.252034794902e-03
  0 KSP unpreconditioned resid norm 2.252034794902e-03 true resid norm 2.252034794902e-03 ||r(i)||/||b|| 1.000000000000e+00
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 19
  1 KSP unpreconditioned resid norm 1.843225742581e-05 true resid norm 1.843225742582e-05 ||r(i)||/||b|| 8.184712539768e-03
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 19
  2 KSP unpreconditioned resid norm 1.410472862037e-09 true resid norm 1.410472860342e-09 ||r(i)||/||b|| 6.263104209294e-07
  Linear fieldsplit_pressure_ solve converged due to CONVERGED_RTOL iterations 19
  3 KSP unpreconditioned resid norm 1.051996270409e-14 true resid norm 1.064465321443e-14 ||r(i)||/||b|| 4.726682393419e-12
Linear solve converged due to CONVERGED_ATOL iterations 3
1 SNES Function norm 1.063917948054e-14

Bibliography

KnepleyBrownRuppSmith13

M. G. Knepley, J. Brown, K. Rupp, and B. F. Smith. Achieving high performance with unified residual evaluation. ArXiv e-prints, September 2013. arXiv:1309.1204.